Edit: The term "bounding square" in this question is shorthand for "the minimal area square that encloses the triangle".
The topic of finding the bounding square of arbitrary triangle has come up a number of times in SEM and in my opinion there has never been a definitive answer and especially I have never seen a method to construct it geometrically using only a compass and a straightedge.
I was beginning to think it was one of those impossible problems like squaring the circle. I now think I have come up with a geometrical method to construct it.
There are 4 cases:
- Only 1 angle of the triangle is $\geq$ 45 degrees.
- Only 2 angles are $\geq$ 45 degrees.
- All 3 angles are > 45 degrees and the altitude of the smallest angle is < the base.
- All 3 angles are > 45 degrees and the altitude of the smallest angle is $\geq$ the base.
Cases 1 and 4 are fairly trivial.
- The bounding square is simply the square constructed with the diagonal of the square being equal to the longest side of the triangle.
- The bounding square is the square with sides equal to the altitude of the smallest angle of the triangle and the shortest side of the triangle lies on a side of the square.
Cases 2 and 3 require a special construction method that can be applied to both cases but in case 2 the vertex of the triangle that coincides with a vertex of the bounding square is the smallest angle and in case 3 the shared vertex is the largest angle.
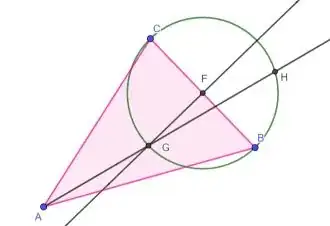
A construction that highlights the minimum area bounding square for any arbitrary triangle is here.
The construction sequence animation is here. The abbreviated construction sequence is:
Construct the perpendicular bisector of the side (BC) opposite the shared vertex (A).
Draw a circle centered on F with radius (BC)/2.
Find the intersection (G) of the perpendicular bisector with circle, that is nearest vertex A.
Draw a ray from A passing through G.
Find the second intersection of the ray and the circle that is outside the triangle (H).
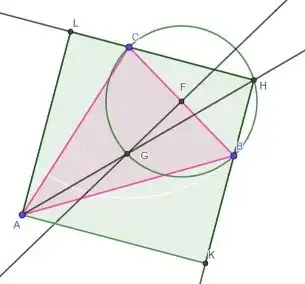
H is the second vertex of the bounding square. (A is the first).
Draw rays from H through the remaining vertices of the triangle.
Draw lines from A perpendicular to rays HL and HK.
I claim the smallest possible bounding minimal area square of the triangle is the square ALHK. I am looking for a proof (or counter-proof) that the algorithm outlined here does in fact produce the smallest bounding square of any given arbitrary triangle.
(My numerical attempt to find the related largest triangle that can be enclosed by a unit square is given in an answer to another question).