1

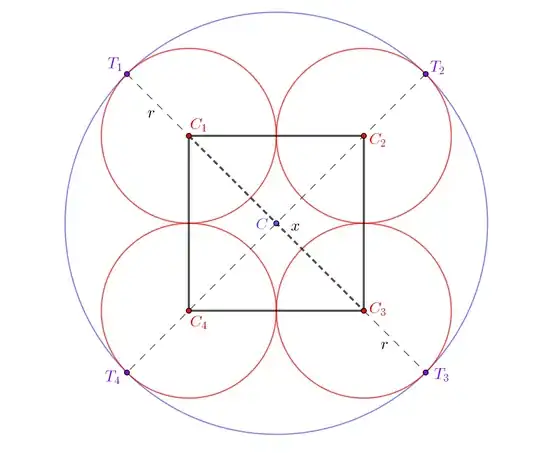
I have two questions provided below about solving area for circles. They're from a previous homework I hadn't done but I wanted to try and do them now so I can prepare for my final. Any help with solving them is appreciated! I just wanted to figure them out now so I had some idea of how to do questions like these on a final.

For question 7, I had the idea that since the center of each circle belongs to the other circle that the overlapping region would be equal to $1/2(\pi r^2)$.

For question 8, I was thinking a similar idea that the diameter of the smaller circles would be equal to $1$ with the radius as $0.5$.

enter image description here

Anton Vrdoljak
  • 2,717
nadelock
  • 31

3 Answers3

1

One possible idea for the question $8$ will be to notice the square (the figure is below) which vertices are centers of the $4$ smaller circles, i.e. points $\,C_1, C_2, C_3, C_4.\,$ It is obvious that $\,|C_1C_2|=|C_2C_3|=|C_3C_4|=|C_4C_1|=2r.\,$ Hence, a diagonal $x$ of this square we can find from right triangle $\,\triangle C_1C_4C_3\,$ i.e. we have: $$ x^2=4r^2+4r^2. $$ Next, it is obvious too that for a diameter of the biggest circle, a radius of a smaller circle $r$ and a diagonal $x$ this relation holds: $\,x=4-2r$.
Hence, we have: $$ 16-16r+4r^2=4r^2+4r^2 \iff 4r^2+16r-16=0\iff \boxed{r=-2+2\sqrt{2}}. $$ Figure: enter image description here

Anton Vrdoljak
  • 2,717
1
  1. If two circles intersect and pass through each others' centers, their centers and either intersection are the vertices of an equilateral triangle having side length equal to their radii. That means the line joining the radii makes a $60^\circ$ angle = $\pi/3$ with a line joining the center to point of intersection. The sector of the circle made of those two lines and the circle is $A_1=(1/2)r^2(\pi/3)=\pi r^2/6$

This includes a right triangle having area $A_2=(1/2)(r/2)(r\sqrt{3}/2)=r^2\sqrt{3}/8$. Removing $A_2$ from $A_1$ is a quarter the overlapping area by symmetry.

The total area held in common is then $A=4(A_1-A2)=r^2(2\pi/3-\sqrt{3}/2)$

  1. The centers of the bottom two circles and the center of the main circle are the vertices of a $45-45-90$ triangle. If $r+x$ is the distance between the center of a smaller circle to the center of the large circle, By the Pythagorean Theorem, $2(r+x)^2=(2r)^2=4r^2$

$r^2+x^2+2rx=2r^2\implies x^2+2rx-r^2=0\implies x=\frac{-2r\pm \sqrt{8r^2}}{2}\implies x = -r \pm r\sqrt{2}$

$\implies x = r(\sqrt{2}-1)$

$2=4r+2x=4r+2r\sqrt{2}-2r=2r(1+\sqrt{2})\implies r = \sqrt{2}-1$. So the area of one small circle is $\pi(3-2\sqrt{2})$

TurlocTheRed
  • 5,683
-1

For question $8$, draw a line from where one of the smaller circles is tangent to the large circle to the centre. Since we have a right triangle with bases $r$ and $r$ where the hypotenuse makes up part of this distance, $r + \sqrt{2}r = 2$.

Thence $r = \frac{2}{1 + \sqrt2} = \frac{2(1 - \sqrt2)}{-1} = 2(\sqrt2 - 1)$ and $\pi r^2 = 4(\sqrt2 - 1)^2 \pi$.

Toby M
  • 81