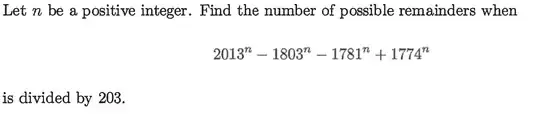I have been preparing for math olympiad recently and I came across this question.
and I looked up for solution and it said
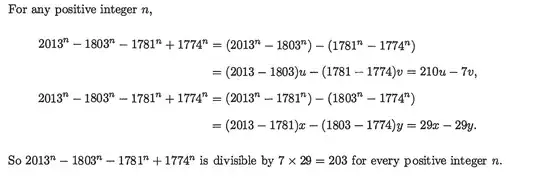
Which I do not understand how the power of unknown such as 2013^n - 1803^n can be represented as (2013-1803)u when u is a polynomial. What is u in this equation and what kind of polynomial is it? Also how does this work?