How can we approximate the median of the numbers in the first $n$ rows of Pascal's triangle? (The top row is the $0$th row.)
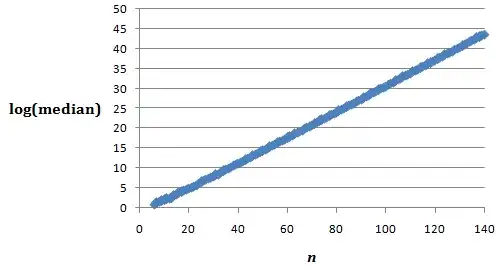
Using Excel, I made a graph of the natural log of the median against $n$, for $n=6$ to $n=140$. (For $n=0$ to $n=5$, the median is $1$.)
I used the points from $n=101$ to $n=140$ to calculate a trendline, and I got $\text{median}\approx 0.126\times1.380^n$ Do the constants have asymptotic closed forms? That $1.380$ is very close to $\ln4\approx1.386$.
Context: I asked my high school students to find the mean of the numbers in the first $n$ rows of Pascal's triangle (the answer is $\frac{2(2^n-1)}{n(n+1)}$). Then I wondered, what about the median? (The mode of the entire triangle, if we ignore the $1$'s, is conjectured to be $3003$.)
EDIT:
If the median of the first $n$ rows is indeed approximately $c\times (\ln4)^n$ for some constant $c$, then we would have the following result:
The median of the first $n$ rows is approximately equal to the central binomial coefficient of row $2k$, where $2k\approx \left(1+\frac{\ln \ln 2}{\ln 2}\right)n\approx 0.47123n$. (So the median is approximately in the middle of the triangle.)
Explanation: The central binomial coefficient of row $2k$ is approximately $\frac{4^k}{\sqrt{\pi k}}$. Setting this equal to $c\times(\ln4)^n$, we get $2k=\frac{ \ln c+\frac12 \ln \pi+\frac12 \ln k +n \ln \ln 4 }{\ln 2}$. So for large $n$, we have $2k\approx \left(1+\frac{\ln \ln 2}{\ln 2}\right)n$.
But I don't know how to show that the median is approximately $c\times (\ln4)^n$ for some constant $c$.