13

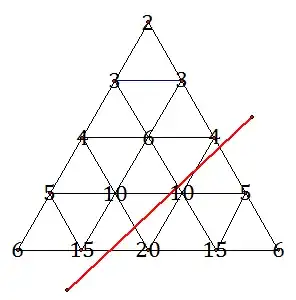
Consider Pascal's triangle with $n$ rows, without the $1$s, with each number corresponding to a vertex on a pyramid of equilateral triangles, as shown below with example $n=5$.

enter image description here

Can the triangle be divided by a straight line (that does not pass through any vertex) into two regions of equal sums?

(That is, does there exist an $n$ such that Pascal's triangle with $n$ rows, without the $1$s, can be divided by a straight line into two regions of equal sums?)

For example, with $n=5$, the red line below fails to divide the triangle into two regions of equal sums: the upper-left region has a sum of $58$, and the bottom-right region has a sum of $56$.

enter image description here

I have tried to do this with different size triangles, without success. It seems that it cannot be done, but I don't know how to prove it.

Remarks

We exclude the $1$s because the triangle with the $1$s has a total sum of $2^n-1$, an odd number, making an equal split obviously impossible.

The sums of the all the terms in the first $n$ rows (not just one row) are given by A145654 (ignoring the initial $0$): $2,8,22,52,114,240,494\dots$

I considered the partial sums of a row of Pascal's triangle, but such expressions are not easy.

I also tried to start with Pascal's triangle without the $1$s and without the terms $\binom{n}{1}$ and $\binom{n}{n-1}$, and I still couldn't split it. However, it is easy to split a triangle with terms $1*1\ 1*1\ 2\ 1*1\ 2\ 2\ 1*1\ 2\ 3\ 2\ 1$ (rows are separated by "$*$"; in each row, numbers increase by $1$ up to a max, then decrease by $1$.).

I'm more interested in the method used to answer this question, than the answer itself. I've been trying to demystify Pascal's triangle, but it still mystifies me.

EDIT:

Taking @Jean Marie's suggestion, I've added a left-justified version of the triangle, which is easier to use.

enter image description here

EDIT2: ​

Dan
  • 22,158
  • 5
    Put a vertical line in the middle ;) – LL 3.14 Nov 28 '23 at 12:28
  • @LL3.14 I edited to clarify that the line does not pass through any vertex. – Dan Nov 28 '23 at 12:33
  • 1
    I have made a computer program with random separating lines : indeed it has found no case of equality. – Jean Marie Nov 28 '23 at 19:34
  • 1
    ... but some cases where the difference is only 2. – Jean Marie Nov 28 '23 at 20:35
  • 1
    I advise you to use the "left-justified" version of the Pascal triangle, as you can see some in the -good- Wikipedia article on Pascal's triangle. This version can be obtained by a linear transformation from the "isosceles" usual form : the image of the separating line will still be a straight line, and the subsequent computations are simpler. – Jean Marie Nov 28 '23 at 21:08
  • @JeanMarie With your computer program, what value(s) of $n$ (number of rows) did you use? – Dan Nov 28 '23 at 21:44
  • 1
    Till $n=21$ if I recall well. – Jean Marie Nov 28 '23 at 21:45
  • @JeanMarie is the usual form an "isosceles" or a proper equilateral? – Older Amateur Nov 29 '23 at 21:59
  • @Older Amateur You are right : it is often presented as an equilateral triangle. – Jean Marie Nov 29 '23 at 22:04
  • 2
    Rotating the triangle through $\frac\pi 2$ radians in increments of $0.0001$ radians and scanning both horizontally and vertically finds no equality for $n<62$ – Daniel Mathias Nov 30 '23 at 04:46
  • You can always get a difference of 2 by choosing one group to be the bottom row, excluding one of the end values. – Dunham Dec 07 '23 at 18:29
  • 1
    Well, there’s less than $n^4$ ways of splitting $n$ rows of Pascal by a line and $2^n$ target splits, and you already checked up to 62,so the probability any triangle works is less than around. $\sum_{n=62} n^4/2^n \approx 2*10^{-12}$, so it’s unlikely for a perfect split to exist. – Eric Dec 08 '23 at 13:33
  • might help to think of it as a $\mathbb{Z}^3$ function with values $(x,y,\binom{x}{y} )$ – vallev Dec 08 '23 at 18:20
  • something like this https://www.desmos.com/3d/8afd2a250f – vallev Dec 09 '23 at 08:24

0 Answers0