Conjecture: Given any $2n+1$ points, we can always draw $n$ non-intersecting circles whose diameter endpoints are $2n$ of those points.

Question

Is the following conjecture true or false:

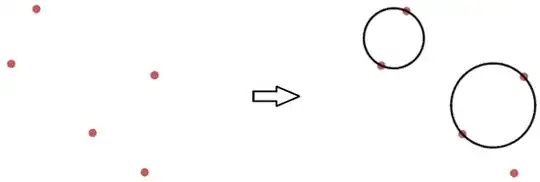
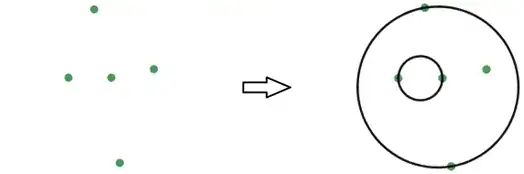
Given any $2n+1$ coplanar points, we can always draw $n$ non-intersecting circles coplanar with the points, whose diameter endpoints are $2n$ of those points.
We consider tangent circles to be non-intersecting.

This is a generalization of my earlier question about the case $n=2$. That question is currently unanswered. I wonder if it is easier to prove the general case.

Example:

Another example:

I cannot find a counter-example, nor can I prove the conjecture.

I made a generator of seven (pseudo)random points.

(If, instead, we were given $2n$ points, the conjecture would not be true: for example, if the $2n$ points were the vertices of a regular $(2n-1)$-gon plus the centre, then we could not draw $n$ non-intersecting circles.)

score 1 · Accepted Answer · answered Nov 19 '23 at 10:49

1

No that's not true for $n=3$. Consider 7 points on the complex plane in such location: one at $0$ and other 6 at $0.01\omega^i,\omega^i, i=0,1,2$, where $\omega$ is the 3-th unit root ($-\frac{1}{2}+\frac{\sqrt{3}}{2}i$).

answered Nov 19 '23 at 10:49

Yutsing

61

Three circles with diameters from $0.01\omega^i$ to $\omega^i$ does it. – B. Goddard Nov 19 '23 at 11:00
2

No they intersect with each other – Yutsing Nov 19 '23 at 11:01

Conjecture: Given any $2n+1$ points, we can always draw $n$ non-intersecting circles whose diameter endpoints are $2n$ of those points.

1 Answers1

Linked