Conjecture: Given any five points, we can always draw a pair of non-intersecting circles whose diameter endpoints are four of those points.

Question

Is the following conjecture true or false:

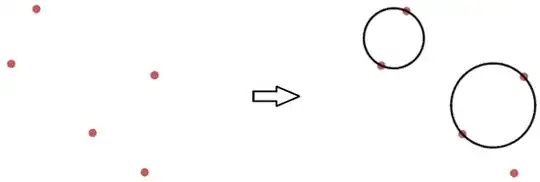
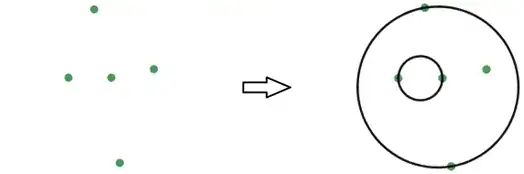
Given any five coplanar points, we can always draw at least one pair of non-intersecting circles coplanar with the points, such that two of the given points are diameter endpoints of one circle, and another two of the given points are diameter endpoints of the other circle.
Tangent circles are considered to be non-intersecting. Coincident circles are considered to be intersecting.

Example:

Another example:

I cannot find a counter-example, nor can I prove the conjecture. I made a generator of five (pseudo)random points.

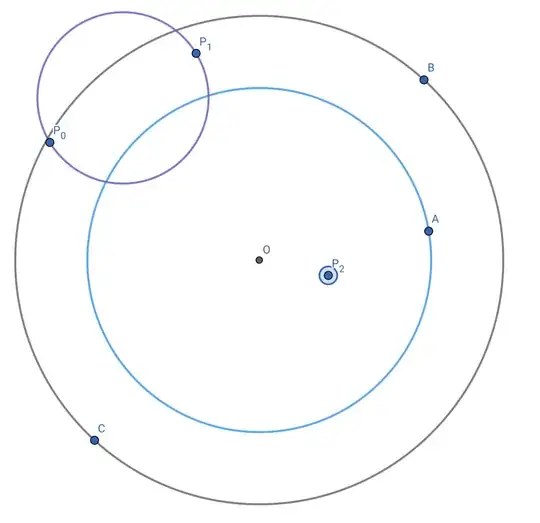
(If, instead, we were given four points, the conjecture would not be true: for example, if the four points were the vertices of an equilateral triangle plus the centre, then we could not draw a pair of non-intersecting circles.)

Context: I was thinking about this question about random points in a disk. Staring at various sets of five points, I came up with this conjecture.

Edit: The generalized conjecture ($2n+1$ points and $n$ circles) is not true.

Edit 2: I have asked, and answered, a similar question. Maybe it might provide ideas for this question.

Edit 3 Posted on MO.

Answer 1

A counterexample is given by the following five points: $$(0,0),(1,0), \Big(-\frac{64867}{77629},\frac{3389}{60094}\Big), \Big(\frac{5981}{56176},\frac{32211}{34172}\Big), \Big(\frac{5925}{117812},-\frac{103221}{116516}\Big).$$

---

Calculations and the way this example was found are presented in this pdf image of a Mathematica notebook. In particular, it is noted there that a certain "defect" of this example, which makes it a counterexample, is very small, about $3\times10^{-6}$. So, here one can have here two "very slightly intersecting" circles, their intersection certainly invisible to the eye if both circles are fully shown.

Answer 2

Here is a way to turn it from geometry into algebra without square-roots. I don't have a solution either.
Given four points $(a,b),(c,d)$ and $(e,f),(g,h)$, we are looking for a point $(x,y)$ on two circles, so two dot products are zero: $$(x-a,y-b).(x-c,y-d)=0\\ (x-e,y-f).(x-g,y-h)=0$$ The difference between these is linear so $(x,y)$ lies on a straight line and can be parameterised as $$(x,y)=\left(\frac{eg-ac+t}{e+g-a-c},\frac{fh-bd-t}{f+h-b-d}\right)$$ where $t$ is free. The two equations at the start become a single quadratic in $t$, and the point $(x,y)$ exists if the discriminant is nonnegative.
The numerator I get for the determinant is
$$-4(eg-ac+fh-bd)^2+((a+c)(f+h)-(e+g)(b+d))^2 +4(e+g-a-c)(eg(e+g)-ac(a+c)) +4(f+h-b-d)(fh(f+h)-bd(b+d))\lt0$$ There are fifteen sets of four points paired up. Is it possible to show not all fifteen discriminants can be positive?

Answer 3

This is just some ideas,

Consider the two points such that the distance between them is maximum, In the diagram, I call those two points $C$ and $B$, we will work in the complex plane with the origin as $O$, the midpoint of $CB$.

There is a special blue circle inside my diagram, centered at $O$ is such that if it had a radius of $1$, then circle $BC$ will have a radius of $\sqrt2$. (Scale accordingly)

This blue circle has the property of if any two points lie within this circle, then the circle formed by these two points necessarily do not intersect with circle $CB$. Proof: Consider any two points inside or on the unit circle call $x,y$ Then the point on the circle formed by $xy$ furthest away from the origin has magnitude: (1) $|(x+y)/2+i(x-y)/2|$ where i is the imaginary unit. Then bound using triangle inequality:

$(1)\le(0.5)(|x||1+i|+|y||1-i|)\le 0.5(2\sqrt2)=\sqrt2$

With this, we see that it is necessary that at most 1 point can lie within the blue circle.

Then I tried to bash 3 cases,

(1) Two points lie outside of circle $CB$.

(2) One point lie outside of circle $CB$ and one between circle $CB$ and the blue circle

(3) Two points lie between circle $CB$ and the blue circle.

I guess a way to approach the rest is to complex bash the magnitudes.

Consider any four complex points, $m,n,q,r$ . Then the circles formed by $mn$ and $qr$ necessarily intersect if

$|(m+n)/2-(q+r)/2|<|(m-n)/2|+|(q-r)/2|$
(Distance beteween the centers)< (The sum of the individual radiuses)

I know that this claim does not work when a circle is contained inside another, that is why I chose $CB$ to be the largest as I conjecture that after the argument above, there should be no circle inside circle configuration.

Partial progress, will edit if there are any more progress.

Answer 4

EDIT 2: One excellent counterexample has been provided by another anwser, the four points of which are nearly a square, resulting in the "very slightly intersecting". I ever tried to find one starting from a square but failed. It turns out my final success was the idea "the example that is 'closest' to an counterexample is the four points of a square together with its center".

---

EDIT: The following "proof" is wrong, so don't care much about it :P

Now I think the example that is "closest" to an counterexample is the four points of a square together with its center. In this case the circles intersect with each other, or are tangent. (However tangent circles are considered to be non-intersecting.)

Given five points, there are ten circles. We can imagine how difficult it is to let them intersect with each other. It is not hard to deal with the first four points, but the fifth point will introduce four more circles and we should consider each of the four intersecting or not with the original six circles. (You may understand better by trying to find an example where only one pair of circles are allowed to intersect with each other.)

---

This is not a proof but just provide some ideas.

Denote the five points as $A,B,C,D,E$. Suppose no three of them are collinear, otherwise the conclusion holds immediately.

First we pick $A,B$ such that they have the minimum distance. Let $P$ be the midpoint of $AB$.
Among $C,D,E$ assume $C$ is the farthest one to $P$. Then we can draw some circles.
In the following figure, the red circles means $D,E$ must be outside them, since $AB$ is the shortest, the green circles means $D,E$ must be inside it, since $C$ is the one farthest from $P$, and the annulus with dashed lines means that $D$ must be inside it if we want the circle with diameter $CD$ intersects with the one with diamter $AB$.

Now we can suppose both $D,E$ are in the annulus. We can observe that only two small regions are left for them. In fact, the actual regions such that circle($CD$ or $CE$) and circle($AB$) intersects is much smaller, and one of them is approximately drawn in black.
If $D,E$ are in the same regions (e.g. both in the black region) then circle($DE$) do not intersect with circle $AB$. If $D,E$ are in different regions then circle($DE$) will cover circle($AB$).

Answer 5

I believe I found a proof, which relies in the following two statements:

1. Given a set of five non-collinear points on the Euclidean plane, it is always possible to find a convex subset of 4 points.

2. Given a convex subset of 4 points on the Euclidean plane, there are always two opposite edges the midpoint of which are separated by a distance equal or larger than the average of their lengths.

From these statements it is possible to do a proof by construction.

The remaining case with three or more collinear points has trivial solution by choosing any two pairs of points on the line and constructing two circles, which will necessarily kiss at the common point.

Sketch proof of theorem 1: Consider three arbitrary non-collinear points on the plane, (p,q,r). Add a fourth non-collinear point, s. If s lies outside the (p,q,r) triangle we found a convex quadrilateral (p,q,r,s). Otherwise, we have decomposed the (p,q,r) triangle into three triangles, (p,q,s), (q,r,s) and (p,r,s). Add a fifth point t. If t lies outside the original (p,q,r) triangle, we found the convex quadrilateral (p,q,r,t). Otherwise, t HAS TO lie inside one of the smaller triangles, say (p,q,s), which in turn means it lies outside both (q,r,s) and (p,r,s), from which we can build either convex quadrilateral (q,r,s,t) or (p,r,s,t).

Answer 6

HINT.- A method to solve this problem with the help of a computer

Five planar points $P_i=(x_i,y_i);\space 1\le i\le5$, been given, the circle having $\overline{P_iP_j}$ as diameter has equation $$x^2+y^2-(x_i+x_j)x-(y_i+y_j)y+x_ix_j+y_iy_j=0$$ It follows that if the given condition is true, then, among the ten possible circles as desired, there are at least two circles either, disjoints or tangents. Since the resultant of two equations $$x^2+y^2-(x_i+x_j)x-(y_i+y_j)y+x_ix_j+y_iy_j=0\quad(1)\\x^2+y^2-(x_h+x_k)x-(y_h+y_k)y+x_hx_k+y_hy_k=0\quad(2) $$ is of the second degree so we need a system of a pair of the ten circles such that the discriminant of their resultant be negative or null (which correspond to disjoint or tangent circles). This is easy to do with fixed five points but for variable ones we rather can use a little program for computer because the algorithm is tedious.