Is this a new point on the nine-point-circle of a triangle?

Question

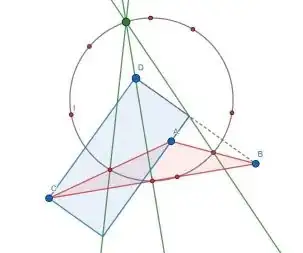
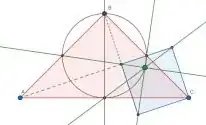
I was trying to get a feel for how to solve another question about the largest triangle that can fit in a unit square, by constructing the smallest enclosing square of a triangle in Geogebra. While doing this I 'discovered' what appears to be a new point on the nine-point circle of a triangle, that relates a rectangle to a triangle via a circle.

Here the intersection with the nine-point-circle is outside both the rectangle and the triangle.

The intersection in this case, is the only point on the nine-point-circle that is entirely within the triangle.

If the triangle is a right triangle and the rectangle is constructed so that side of the rectangle lies on the midpoint between the shared vertex and the right angle, the rectangle is a square.

The point is very easy to construct. Construct a rectangle such that each of the (possibly extended) sides lies on a vertex of the triangle. Since there are 4 vertices on the rectangle and only 3 on the triangle, the rectangle and triangle must always have a vertex in common. Now draw lines from each of the unshared vertices of the rectangle to the midpoint of the associated side of the triangle. These 3 lines will always intersect at a point that lies on the nine-point-circle of the triangle, although I cannot prove that formally.

This remains true even if the rectangle overlaps the triangle or is smaller that the triangle.

I think this point is interesting because it shows how a triangle and a rectangle and a circle are related, and I have never seen a triangle centre or point on a nine-point-circle constructed like this before.

Here is a link to an interactive construction uploaded to the Geogebra website. Any of the blue points on the construction can be moved.

I cannot relate this point to any other well know centre or line of a triangle. At the moment the point can only be found by constructing the rectangle first. If it was possible to construct the point independently, it could be helpful in constructing the smallest possible enclosing square of a given triangle and help answer the question posed by the other member.

Wondering if this is a new point I found an online Encyclopaedia of Triangles but have no idea how to search that database. Is it new? Has anyone seen it before and does it have a name?

Answer 1

Here's a proof for a particular configuration. (Adjusting it for generality is left as an exercise to the reader.)

---

Let rectangle $\square AFDE$ circumscribe $\triangle ABC$, with $B$ and $C$ on $\overline{FD}$ and $\overline{DE}$, respectively. Let $A'$, $B'$, $C'$ be the midpoints of $\overline{BC}$, $\overline{CA}$, $\overline{AB}$, and let lines $\overleftrightarrow{DA'}$ and $\overleftrightarrow{EB'}$ meet at $P$.

Note that $|A'B|=|A'C|=|A'D|$ and $|B'C|=|B'A|=|B'E|$. (Why?) Then, a little angle-chasing shows that $\angle A'PB'\cong\angle C = \angle A'C'B'$. Thus, points $A'$, $B'$, $C'$, $P$ are concyclic, lying on $\bigcirc A'B'C'$, the Nine-Point Circle.

We can argue similarly about the intersection of lines $\overleftrightarrow{DA'}$ and $\overleftrightarrow{FC'}$, so that $P$ must be the point of concurrence of all three such lines. $\square$

Answer 2

Let $CA_1C_1B_1$ be a circumscribed rectangle to triangle $ABC$ with common vertex in $C$.

Here is a simple analytical proof :

• 1. showing the validity of your construction of point $M$ (the fact that straight lines $A_1A',B_1B',C_1C'$ meet in a common point).
• 2. showing that $M$ belongs to the nine-points circle.

Part 1

Let us take a system of coordinates where $C$ is the center and $x$ and $y$ axes are defined by $\vec{CA_1}$ and $\vec{CB_1}$ resp. Let

$$A_1=(a,0), \ \ B_1=(0,b), \ \ C_1=(a,b).$$

$$\text{and} \ A=(\lambda a,b), \ \ B=(a,\mu b)$$

where $\lambda$ and $\mu$ can take any value (on the figure, they belong to interval $(0,1)$ but it can be any real value, covering in this way all the cases shown in the question).

With these notations, the equations of lines $A'A_1$ and $B'B_1$ are :

$$\begin{cases}b x+\lambda a y &=&\lambda a b\\ \mu b x+a y &=&\mu a b\end{cases}$$

Let us define $M$ as the intersection of these lines. Solving the system above, we get the coordinates of point $M$ :

$$M=\left(x_M=a \frac{\lambda(\mu-1)}{\lambda \mu -1}, y_M=b \frac{\mu(\lambda-1)}{\lambda \mu -1}\right)$$

Having these coordinates, it is not difficult to show that $M,C',C_1$ are aligned, ending part 1 of the proof.

Part 2 : In this system of coordinates, the equation of the 9-point circle is of the form :

$$-2ux-2vy+w+(x^2+y^2)=0,$$

Let $X(x,y)$ be the generic point of 9-point circle. Let us express that $A',B',C',X$ are concyclic, i.e., that their coordinates verify

$$\begin{cases} -2ux_{A'}-2vy_{A'}+w+(x_{A'}^2+y_{A'}^2)&=&0\\ -2ux_{B'}-2vy_{B'}+w+(x_{B'}^2+y_{B'}^2)&=&0\\ -2ux_{C'}-2vy_{C'}+w+(x_{C'}^2+y_{C'}^2)&=&0\\ -2ux-2vy+w+(x^2+y^2)&=&0\\ \end{cases}$$

These four constraints can be expressed under the following form :

$$\underbrace{\begin{pmatrix}a&\mu b&1&(a^2+\mu^2b^2)\\ \lambda a&b&1&(\lambda^2 a^2+b^2)\\ (\lambda+1)a&(\mu+1)b&1&((\lambda +1)^2 a^2+(\mu+1)^2 b^2)\\ 2x&2y&1&4(x^2+y^2) \end{pmatrix}}_P \underbrace{\begin{pmatrix}-u\\-v\\w\\1/4\end{pmatrix}}_V=\begin{pmatrix}0\\0\\0\\0\end{pmatrix}\tag{1}$$

Homogeneous system (1) has a non trivial solution $V$ if and only if the determinant of matrix $P$ (as defined above) is zero, giving an expression involving indeed a second degree polynomial in $x,y$.

Now, it remains to check that replacing $(x,y$) by $(x_M,y_M)$ still gives a zero determinant. This can be done by using a CAS (Computer Algebra System). It is what I have done with a little SAGE script (I can give details).

This $4 \times 4$ determinant equal to $0$ can be brought to this $3 \times 3$ form (by subtracting rows 1 and 2 to row 3, then adding the new row 3 to all other rows, then make a Laplace expansion) :

$$\det \pmatrix{a&\mu b&(a^2+\mu ^2b^2+\nu)\\ \lambda a&b&(\lambda^2a^2+b^2+\nu)\\ 2x&2y&(x^2+y^2+\nu)}=0 \ \ \text{with} \ \ \nu:=2(\lambda a^2+\mu b^2)$$

This equation can be further simplified under the following form :

$$x^2+y^2+\nu-\frac{2}{ab(1-\lambda \mu)}\left(bx \ \ ay\right) \pmatrix{1 & (-\mu)\\(- \lambda ) & 1}\pmatrix{a^2+\mu^2b^2+\nu\\b^2+\lambda^2a^2+\nu}=0$$

Now, the final question : can $M$ be considered as a point-center ? I would say no because of its dependence upon the chosen enclosing rectangle.