9

I made up the following family of sequences: $a_1\in\mathbb{Z}$ and $a_n=\sec (a_{n-1})$ for $n>1$.

I conjecture that, for any $a_1\in\mathbb{Z}$, the proportion of positive terms approaches $\frac{1}{\sqrt {2\pi}}$ as $n\to\infty$. Is my conjecture true?

Evidence for my conjecture

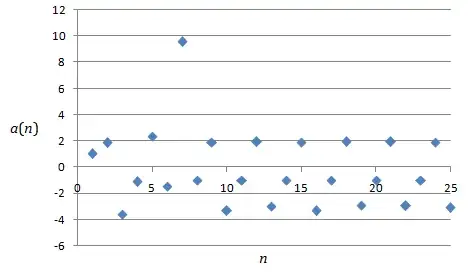
For $a_1=1$, here is the graph of $a_n$ against $n$ for $1\le n \le 25$.

enter image description here

Using Excel, it seems that, the proportion of positive terms approaches a limit as $n\to\infty$, and the limit is independent of the value of $a_1$.

I found that, for $a_1=1, 2, 3, \dots, 25$, among the first $10000$ terms, the average proportion of positive terms is $0.398940$, which is very close to $\frac{1}{\sqrt {2\pi}}\approx 0.398942$.

Another look at the sequence

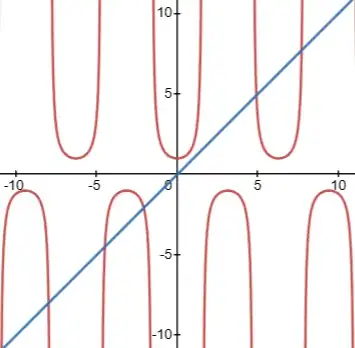
Here are the graphs of $y=\sec x$ and $y=x$.

enter image description here

We start at $(1,\sec 1)$, then go horizontally to the line $y=x$, then go vertically to the curve $y=\sec x$, then go horizontally to the line $y=x$, etc. Among the points that we meet on the curve $y=\sec x$, about $0.39894$ of them are above the $x$-axis.

Dan
  • 22,158
  • 1
    Possibly related: If $a_1=1, a_n=|\cot a_{n-1}|$, then what is $\lim\limits_{n\to\infty}\text{median}{a_1,a_2,\dots,a_n}$? – Dan Oct 06 '23 at 21:58
  • 5
    The function $f(x)=\sec x$ should have some invariant measure (in the sense of ergodic theory) associated to it, and presumably that measure assigns mass $1/\sqrt{2\pi}$ to the set $(0,\infty)$. That should prove the claim for almost all starting values; I'm not sure what additional fact needs to be established about integer starting points to have this apply to them (non-periodic at least). – Greg Martin Oct 06 '23 at 22:19
  • One possible problem with your claim is that $/2\pi$ is transcendental and irrational while the ratio is clearly rational, hence they can never be the same. – Cye Waldman Oct 07 '23 at 22:51
  • 2
    @CyeWaldman A sequence of all rational terms can converge to a transcendental number. For example, the sequence $a_n=\sum\limits_{k=0}^n\frac{(-1)^k}{2k+1}$ converges to $\pi/4$. – Dan Oct 08 '23 at 02:07
  • @Dan Of course, but in this case there is no such summation, it's just a single number that is the ratio of the number of positive outcomes to the total number of trials. I've done this numerically out to &n=10^8&. The results are consistently close to, but less than $1/2\pi$. – Cye Waldman Oct 08 '23 at 13:17
  • It is very likely that the $\sqrt{2\pi}$ is obtained by sheer coincidence. My calculations for ~1000000 iterations show that the ratio is around 40 percent. This might be easier to explain, since for example the last five elements of the set of 1000000 iterations for $a_1=2$ are $-1.00244, 1.85787, -3.53176, -1.08126, 2.12669$ – polfosol Oct 09 '23 at 16:39
  • My point is, if you take 5 elements of this sequence, there is a good possibility that exactly two of them are positive. – polfosol Oct 09 '23 at 16:44
  • @polfosol Are you suggesting that the limit is $2/5$ ? – Dan Oct 09 '23 at 22:32
  • 2
    My computation with $10^8$ terms (using machine precision) shows that the proportion of the positive terms among $a_1,a_2,\ldots,a_n$, with $n$ large enough, is consistently around $0.39885\textsf{x}$, whereas we have $\frac{1}{\sqrt{2\pi}}\approx0.398942$. So I guess the limiting proportion, if exists, is different from $\frac{1}{\sqrt{2\pi}}$. It is also interesting that the distribution of the values of $a_n$ is very complicated and fractal-like. – Sangchul Lee Oct 10 '23 at 01:03
  • Posted on MO. – Dan Oct 16 '23 at 05:35

0 Answers0