Here is a conditional result, providing a candidate for the value of the limit.
Let $x_1 = 1$ and $x_{n+1} = \cot x_n$. Since $\cot$ is an odd function, we have $|x_n| = a_n$ for all $n$. Based on some numerical experiments, we make the following ansatz:
Assumption. The empirical probability measure $\mu_N = \frac{1}{N} \sum_{n=1}^{N} \delta_{x_n}$ converges weakly to the centered Cauchy distribution $\mu$ with shape parameter $\gamma > 0$, that is,
$$ \mu_N(\mathrm{d}x) \to \mu(\mathrm{d}x) = \frac{\gamma}{\pi(x^2 + \gamma^2)} \, \mathrm{d}x. $$
Under this assumption, for $x > 0$ we have
$$ \mathbf{P}_{X\sim \mu_N}(|X| \leq x) \to \mathbf{P}_{X\sim\mu}(|X| \leq x) = \frac{2}{\pi}\arctan\left(\frac{x}{\gamma}\right), $$
and then it can be proved that
\begin{align*}
[\text{median of $\{a_1,\ldots,a_n\}$}]
&= [\text{median of $|X|$, where $X \sim \mu_N$}] \\
&\to [\text{median of $|X|$, where $X \sim \mu$}]
= \gamma.
\end{align*}
So it suffices to determine the value of $\gamma$. To this end, consider a random variable $X \sim \mu$. Then $\cot X$ has the same distribution as $X$. By comparing the PDF of $X$ and $\cot X$, we get
\begin{align*}
\frac{\gamma}{\pi(x^2 + \gamma^2)}
= \frac{1}{1+x^2} \sum_{k\in\mathbb{Z}} \frac{\gamma}{\pi((\operatorname{arccot} x + k \pi)^2 + \gamma^2)}
= \frac{\coth \gamma}{\pi(x^2 + \coth^2 \gamma)}.
\end{align*}
Therefore $\gamma$ must satisfy $\gamma = \coth \gamma$. This equation has a unique positive solution with the value
$$ \gamma \approx 1.1996786402577338339, $$
which agrees with the numerical observation made by other users.
Addendum. Below is the probability histogram of first $10^4$ terms of $(x_n)$ and the graph of PDF of the limiting
Cauchy distribution $\mu$:

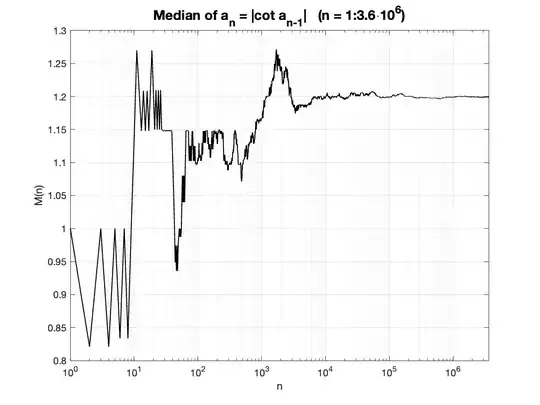
Caution. Numerical simulation are not totally suited for probing the behavior of the median.
This is because the sequence $(x_n)$, hence $(a_n)$, is very susceptible to small numerical errors, which is significantly amplified when a term gets close to one of the poles of $\cot$. (This is essentially due to loss of significance.)
For instance, simulating $n \mapsto \text{median}(a_1,\ldots,a_n)$ using machine precision and $10000$-digit precision shows fairly different behavior even starting around $n = 20$: