Sums of three cubes of form $a^3+b^3+c^3=(c+1)^3$?

Question

Let all variables be positive integers. Consider the forms,

$$a^2+b^2=(b+1)^2\tag1$$ $$a^3+b^3+c^3=(c+1)^3\tag2$$

The smallest solutions are the well-known,

$$3^2+4^2=5^2$$ $$3^3+4^3+5^3=6^3$$

All solutions of Eq.1 are covered by only one polynomial parameterization. On the other hand, not all solutions of Eq.2 are covered by its three known parameterizations.

---

I. Family 1

$$(3 n^2)^3 + (6 n^2 - 3n + 1)^3 + (9 n^3 - 6n^2 + 3n - 1)^3 = (9 n^3 - 6n^2 + 3n)^3$$

$$3^3 + 4^3 + 5^3 = 6^3\\ 12^3 + 19^3 + 53^3 = 54^3\\ 27^3 + 46^3 + 197^3 = 198^3$$

Note: $F(n) = (6, 54, 198)/6 = 1, 9, 33,\dots$ is A005920, or the "tricapped prism numbers".

---

II. Family 2

$$(3 n^2)^3 + (6 n^2 + 3n + 1)^3 + (9 n^3 + 6n^2 + 3n)^3 = (9 n^3 + 6n^2 + 3n + 1)^3$$

$$3^3 + 10^3 + 18^3 = 19^3\\ 12^3 + 31^3 + 102^3 = 103^3\\ 27^3 + 64^3 + 306^3 = 307^3$$

Note: $F(n) = (18, 102, 306)/3 = 6, 34, 102,\dots$ is A067389.

---

III. Family 3

$$(n)^3 + (3n^2 + 2n + 1)^3 + (3n^3 + 3n^2 + 2n)^3 = (3n^3 + 3n^2 + 2n + 1)^3$$

$$1^3 + 6^3 + 8^3 = 9^3\\ 2^3 + 17^3 + 40^3 = 41^3\\ 3^3 + 34^3 + 114^3 = 115^3$$

Note: $F(n) = 3n^3 + 3n^2 + 2n = 8, 40, 114,\dots$ is A143943, or "the Wiener index of a chain of $n$ squares".

---

Update: (Jan 22, four months later)

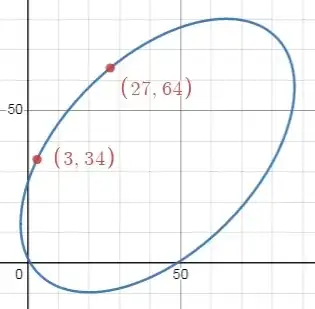
Courtesy of an insight by Adam Bailey in this post, given $x^3+y^3+z^3=(z+1)^3$ we now realize that $(x,y)$ of Family 2 and 3 are just lattice points on the same ellipse. Do the substitution, $z = (k + 1)(x - 1) + k y\,$ where $k = \dfrac{3n^2+1}{3n}$ and, after removing a trivial factor, we get the ellipse,

$$3n^2(x^2 - xy + y^2) - (1 + 6n + 12n^2 + 18n^3 + 9n^4)x - (1 + 3n^2 + 9n^4)y + (1 + 3n + 9n^2 + 9n^3 + 9n^4) = 0$$

where two lattice points are $(x_1, y_1)$ and $(x_2, y_2)$ from Family 2 and 3, respectively. For example, let $n=3$ so,

$$27(x^2 - x y + y^2) - 1342x - 757y + 1063 = 0$$

which for this $n$ has only 2 lattice points,

thus we can use these coordinates,

$$27^3 + 64^3 + 306^3 = 307^3\;\\ 3^3 + 34^3 + 114^3 = 115^3$$

and so on for infinitely other $n$.

---

IV. Unknown Families?

$$14^3 + 23 ^3 + 70^3 = 71^3\\ 21^3 + 46^3 + 188^3 = 189^3\\ 16^3 + 51^3 + 213^3 = 214^3\\ \;9^3 \,+\, 58^3 + 255^3 = 256^3\\ 15^3 + 64^3 + 297^3 = 298^3$$

These and the families above are the primitive solutions with $c<307$.

---

V. Similar equalities

By reverse-engineering those identities,

$$(an^2+bn+c)^3+(dn^2+en+f)^3+(pn^3+qn^2+r)^3=(pn^3+qn^2+rn+s)^3$$

collecting powers of $n$, equating everything to zero, it seems those three are the only quadratic-cubic identities. Turns out there is also the form $a^3+b^3+c^3 = (c\color{blue}{+3})^3$,

$$(m^2)^3 + (2 m^2 + 3m + 3)^3 + (m^3 + 2m^2 + 3m)^3 = (m^3 + 2m^2 + 3m \color{blue}{+3})^3$$

$$(m^2)^3 + (2 m^2 - 3m + 3)^3 + (m^3 - 2m^2 + 3m \color{blue}{-3})^3 = (m^3 - 2m^2 + 3m)^3$$

which, for $m=3n$, can be factored out into $a^3+b^3+c^3 = (c+1)^3$.

---

VI. Question

Just like $a^3\pm b^3 \pm c^3 = 1$ has infinitely many polynomial parameterizations (where degrees are getting higher and higher), does $a^3+b^3+c^3 = (c+1)^3$ also have other families with degree higher than the cubic polynomials in this post?

Answer 1

I’ve produced $4405$ solutions to $a^3+b^3+c^3=(c+1)^3$.

Of these $293$ are of Family 1, $(3n^2,6n^2−3n+1,9n^3−6n^2+3n−1)$

Of these $292$ are of Family 2, $(3n^2,6n^2+3n+1,9n^3+6n^2+3n)$

Of these $216$ are of Family 3, $(n,3n^2+2n+1,3n^3+3n^2+2n)$

That leaves $3604$ to be classified. I’ve moved the $128$ cases, where there are pairs of solutions with equal $c$, to a new question, $a^3+b^3+c^3=(c+1)^3=A^3+B^3+c^3$ solutions. where I found

I’ve found $8$ cases of a new Family 4,

$$a=9n^3$$

$$b=27n^4+18n^3+9n^2+3n+1$$

$$c=81n^6+81n^5+54n^4+27n^3+9n^2+3n$$

And $8$ cases of a new Family 5, $(A,B,c)$

$$A=9n^3+9n^2+3n+1$$

$$B=27n^4+18n^3+9n^2+3n$$

$$c=81n^6+81n^5+54n^4+27n^3+9n^2+3n$$

So, $a^3+b^3+c^3 = (c+1)^3$ DOES also have other families with degree higher than the cubic polynomials in this post.

However, this just scratches the surface, there is plenty of life left in this question.

Answer 2

Here is a further parametric solution, call it Family 6:

$\qquad a=27n^4+54n^3+45n^2+19n+3$

$\qquad b=54n^4+81n^3+63n^2+23n+4$

$\qquad c=243n^6+567n^5+675n^4+468n^3+201n^2+49n+5$

$\qquad c+1 = 243n^6+567n^5+675n^4+468n^3+201n^2+49n+6$

Alternatively,

$\qquad a= (3n + 1)(9n^3 + 15n^2 + 10n + 3)$

$\qquad b= (3n + 1)^2(6n^2 + 5n + 3) + 1$

$\qquad c= (3n + 1)^2(9n^2 + 9n + 5)(3n^2 + 2n + 1) $

$\qquad c+1 = (3n + 1)^2(9n^2 + 9n + 5)(3n^2 + 2n + 1) + 1$

It intersects with Families 1 and 3 when $n=0$ and $n=-1$ respectively.

---

I found this solution by starting from the general parametric integer solution of $x^3+y^3+z^3=t^3$ due to Choudhry (1) and searching for a condition on the parameters that would ensure the necessary difference of $1$. Choudhry’s solution (with a change of letters) is:

$\qquad sx=r(-p^3-q^3+r^3)$

$\qquad sy=-p^4+2p^3q-3p^2q^2+2pq^3-q^4+(p+q)r^3$

$\qquad sz=p^4-2p^3q+3p^2q^2-2pq^3+q^4+(2p-q)r^3$

$\qquad st=r(p^3+(p-q)^3+r^3)$

To limit the search to manageable proportions, I set $r=1$ and looked for solutions with $x,y < 0$, $z,t > 0$ and $-y+1=z$. The point of the latter is that $x^3+y^3+(-y+1)^3=t^3$ can be rearranged as $(-x)^3+t^3+(-y)^3=(-y+1)^3$ with all terms positive, while $sy+sz=3pr^3=s(y-y+1)=s$, so (with $r=1$) the required common factor $s$ must equal simply $3p$. Aiming for $t=z+1$ looks more complicated.

For $3p$ to be a common factor it suffices that $3|p$ and $3p|(q^3-1)$. This can be seen by re-writing Choudhry’s solution (with $r=1$) as below:

$\qquad sx=-p(p^2)-(q^3-1)$

$\qquad sy= -p^2(p^2-2pq+3q^2)+3pq^3-(p+q)(q^3-1)$

$\qquad sz=p^2(p^2-2pq+3q^2)-(2p+q)(q^3-1)$

$\qquad st=2p(p^2)+3pq(-p+q)-(q^3-1)$

To satisfy $3|q^3-1$ it suffices to put $q=3n+1$ implying $q^3-1=27n^3+27n^2+9n$. Putting $p=(27n^3+27n^2+9n)/3n=9n^2+9n+3$ we then have both $3|p$ and $3p|q^3-1$.

It is then straightforward to substitute for $p$ and $q$ in the above rewritten solution and make the identification $(a,b,c,c+1)=(-x,t,-y,z)$ yielding the parametric form for Family 6 above.

This method can perhaps be adapted to find further families of solutions.

Reference:

1. Choudhry A (1998) On Equal Sums of Cubes Rocky Mountain Journal of Mathematics Vol 28(4) p 1256

Answer 3

Partial answer

First, a prime must be chosen. We pick $7$. Then $7$ is decomposed the following way:
$7=1+6=2+5=3+4$
This decomposition is unique to this prime. In this case we need to consider the $3$ cases and find possible soltions. I chose to start with $3+4$ because it's a solution in the first family.
We are looking for a solution of the form:

$3^3 + 4^3 = a^3 - b^3= (a-b)(a^2 +ab + b^2)$

Since $a-b=1$ or $a=b+1$, the equation becomes: $3^3 + 4^3 =a^2 + ab +b^2$ which after substitution of $a$ by $b+1$ becomes: $3^4 + 4^3 =91=3b^2 + 3b +1$, a simple quadratic equation.

$3b^2 + 3b +1= 91$ becomes $3b^2 + 3b +90 =0$ or $b^2 +b - 30=0$, basically a triangular number in disguise.
The solutions are $b=5$ and $b=-6$. Using this values we can write the solution involving both $a$ andd $b$ as:

$3^3 + 4^3 + 5^3 = 6^3$ which is the first equation of the first family.

Next we consider the decomposition $7=2+5$. The equation in $b$ is given by:
$b^2 + b -44 = 0$. The determinant $\Delta$ is not a square in this case so there will not be an integer solution for $(a,b)$.

Last, the decomposition $1+6$ is considered. Following the same steps above, we end up with the quadratic: $b^2 + b - 216=0$ whose solutions are $8$ and $-9$. The equation becomes: $1^3 +6^3 + 8^3 =9^3$ which is the first solution of the third family.

We can consider any prime and do a decompisition and find the corresponding cubic forms. For example, if we consider the prime $37$, we will end up with the following decompositions:
$37=3+34$ and $14+23$.
These decompositions will give us the third and first solution of the third family and fourth family.
If we consider the prime $67$, we will end up, among many solutions, with the $3$ following solutions of the forth family namely:

$21 + 46=67$
$16 + 51=67$
$9 + 58 =67$

This method doesn't distinguish between the families because it uses a quadratic equation to find the solutions. Here again, the triangular numbers keep showing up when they are the least expected.

In fact the method can be generalized to composites to solve $a^3 + b^3 +c^3= d^3$ with $d=c+2$, or $d=c+4$...We will give only one example.

The equation $a^3-b^3=(a-b)(a^2 +ab + b^2)$ becomes:

$2[(b+2)^2 +(b(b+2) +b^2]=6b^2 +12b + 8$

If we take the first equation of the first family, we get:

$3^3 + 5^3 = 152 = 6b^2 + 12b +8$ which becomes:

$6b^2 + 12b -144 =0$

a quadratic with the solutions $b=-6,4$. This equation corresponds to the decomposition of $8$ into $3+5$. Other decompositions of 8 may or may not admit integer solutions.

So again, we see that the method can handle other cases than $d=c+1$ and can use primes or composites as a starting point. The choice of $8$ in the previous example was used just to show that the method works. In general, the starting point is always an integer and its decomposition into a series of two numbers $N=x_{1} +x_{2}$ then using a quadratic derived from the condition $d = c+i$, with $i=1,2,3...$

Answer 4

Numerical solutions of $A^3+B^3+C^3=(C+1)^3$ arranged by $C$. There are nine pairs curiously with the same $C$, namely (255, 477, 1331, 8898, 13088, 14526, 18755, 20154, 22968), a sample of which,

\begin{align} 51^3+82^3+477^3 &= 478^3\\ 4^9+75^3+477^3 &= 478^3\\[4pt] 9^9 + 502^3 + 13088^3 &= 13089^3\\ 16^3 + 801^3 + 13088^3 &= 13089^3\\[4pt] 7^9 + 840^3 + 14526^3 &= 14527^3\\ 294^3 + 847^3 + 14526^3 &= 14527^3\\[4pt] 10^9 + 381^3 + 18755^3 &= 18756^3\\ 1018^3 + 69^3 + 18755^3 &= 18756^3 \end{align}

(3,4,5,6) (1,6,8,9) (3,10,18,19) (2,17,40,41) (12,19,53,54) (14,23,70,71) (12,31,102,103) (3,34,114,115) (21,46,188,189) (27,46,197,198) (16,51,213,214) (4,57,248,249) (22,57,255,256) (9,58,255,256) (15,64,297,298) (27,64,306,307) (58,75,453,454) (5,86,460,461) (64,75,477,478) (51,82,477,478) (20,89,487,488) (48,85,491,492) (57,82,495,496) (61,90,564,565) (66,97,632,633) (58,105,671,672) (48,109,684,685) (6,121,768,769) (91,120,909,910) (23,140,958,959) (75,136,989,990) (7,162,1190,1191) (75,166,1290,1291) (44,173,1324,1325) (136,141,1331,1332) (37,174,1331,1332) (76,171,1346,1347) (8,209,1744,1745) (108,199,1745,1746) (96,205,1779,1780) (149,212,2068,2069) (187,192,2130,2131) (108,235,2178,2179) (148,225,2208,2209) (66,247,2262,2263) (9,262,2448,2449) (118,279,2790,2791) (147,274,2813,2814) (10,321,3320,3321) (52,321,3327,3328) (147,316,3402,3403) (22,327,3414,3415) (248,275,3466,3467) (18,349,3764,3765) (48,355,3866,3867) (131,356,3973,3974) (67,372,4154,4155) (28,375,4193,4194) (192,361,4247,4248) (11,386,4378,4379) (270,343,4473,4474) (241,366,4583,4584) (146,395,4645,4646) (192,409,5016,5017) (232,399,5033,5034) (145,426,5175,5176) (335,368,5398,5399) (131,446,5506,5507) (12,457,5640,5641) (243,460,6101,6102) (165,478,6156,6157) (49,522,6888,6889) (243,514,7074,7075) (13,534,7124,7125) (305,506,7255,7256) (24,547,7386,7387) (225,538,7463,7464) (426,451,7506,7507) (376,495,7625,7626) (205,558,7796,7797) (246,571,8186,8187) (456,475,8205,8206) (97,594,8376,8377) (300,571,8429,8430) (448,519,8750,8751) (421,540,8795,8796) (14,617,8848,8849) (115,618,8898,8899) (72,619,8898,8899) (261,616,9156,9157) (314,605,9172,9173) (434,557,9211,9212) (90,643,9426,9427) (139,648,9570,9571) (300,631,9630,9631) (361,636,10071,10072) (114,673,10104,10105) (282,667,10314,10315) (100,693,10548,10549) (485,614,10732,10733) (15,706,10830,10831) (549,598,11244,11245) (363,694,11285,11286) (542,611,11362,11363) (513,634,11399,11400) (564,595,11402,11403) (493,654,11540,11541) (216,775,12590,12591) (363,760,12738,12739) (587,674,13018,13019) (502,729,13088,13089) (16,801,13088,13089) (190,801,13175,13176) (289,798,13320,13321) (264,823,13854,13855) (319,822,13998,13999) (333,820,14003,14004) (288,835,14213,14214) (627,712,14229,14230) (343,840,14526,14527) (294,847,14526,14527) (432,829,14723,14724) (318,865,15048,15049) (17,902,15640,15641) (621,802,15867,15868) (415,888,16038,16039) (432,901,16452,16453) (390,913,16536,16537) (467,902,16690,16691) (82,951,16937,16938) (216,997,18267,18268) (408,985,18471,18472) (18,1009,18504,18505) (547,954,18546,18547) (381,1000,18755,18756) (69,1018,18755,18756) (507,976,18797,18798) (522,979,18978,18979) (655,948,19433,19434) (619,978,19770,19771) (589,990,19787,19788) (643,984,20154,20155) (594,1003,20154,20155) (808,885,20171,20172) (305,1064,20272,20273) (618,1009,20520,20521) (673,990,20616,20617) (507,1054,20826,20827) (58,1095,20921,20922) (648,1015,20958,20959) (367,1086,21057,21058) (774,967,21353,21354) (45,1114,21467,21468) (19,1122,21698,21699) (496,1095,21870,21871) (823,990,22566,22567) (7,1152,22574,22575) (798,1015,22758,22759) (847,984,22806,22807) (865,978,22968,22969) (822,1009,22968,22969) (840,1003,23106,23107) (913,954,23304,23305) (888,979,23370,23371) (588,1135,23561,23562) (911,980,23785,23786) (535,1158,23846,23847) (411,1192,24242,24243) (20,1241,25240,25241) (370,1251,25874,25875) (588,1219,25914,25915)

If anybody could remind me how to produce LF I'll do it.

Answer 5

We explore solving the equation for a given value of $c$.

Start by expanding the binomial power $(c+1)^3$ and rearranging:

$a^3+b^3=3c^2+3c+1$

Let $3c^2+3c+1=pq$ for any divisor $p$ of $3c^2+3c+1$. Then we have

$a+b=p$

$a^2-ab+b^2=(a+b)^2-3ab=q$

and thus

$ab=(p^2-3q)/3.$

Factors of $3c^2+3c+1$ are all $\equiv1\bmod3$, so $ab$ will properly be an integer. But $p$ must be chosen large enough to render this product positive yet small enough for the discriminant

$\Delta=(a+b)^2-4ab=(a-b)^2$

to be nonnegative. Thus

$(3c^2+3c+1)^{1/3}\le p\le[(3/4)(3c^2+3c+1)]^{1/2}.$

Solutions are then obtained for those cases where $\Delta$ is a square and thus $a-b$ may be rendered a whole number.

Let us drop in $c=70$ as an example. Then $3c^2+3c+1=14911=13×31×37$, and we have potenially eight choices for $p$ (and thus $q$). But $p=13$ is too small to render a positive value for $ab$ and $p=13×31$ is too large giving a negative $\Delta$. Therefore the only possible solutions are given by $p=31$ or $p=37$.

For $p=31$ we calculate:

$q=13×37=481$

$ab=(31^2-481)/3=160$

$\Delta=31^2-(4×160)=321.$

The discriminant, divisible only by $3$ and not by $9$, fails to be a square.

For $p=37$, however:

$q=13×31=403$

$ab=(37^2-403)/3=322$

$\Delta=37^2-(4×322)=81=9^2.$

So we accept $a+b=p=37$ and $a-b=9$, giving the quoted solution $23^3+14^3+70^3=71^3$.