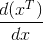0

I'm new to matrix calculus, and I'm confused about how to differentiate a vector $x$'s transpose w.r.t. itself. $\left(i.e. \dfrac{\partial(x^T)}{\partial x}\right)$

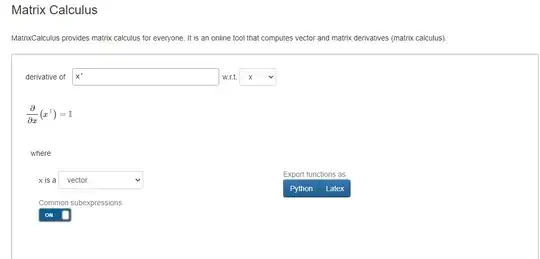
How would one calculate this derivative? From matrix calculator (https://www.matrixcalculus.org/) the result is I (identity matrix), but I can't figure out why. Suppose $x$ is a $n×1$ column vector and $x^T$ is a $1×n$ row vector, since $\frac{\partial }{\partial x}$ = $\left[\frac{\partial }{\partial x_{1}}, \frac{\partial }{\partial x_{2}},\ldots \frac{\partial }{\partial x_{n}}\right]$ , wouldn't $\dfrac{\partial (x^T)}{\partial x} = \dfrac{\partial }{\partial x}⊗x^T$ be a $1×n^2$ row vector instead of the $n×n$ identity matrix? I'm very confused and I don't know which part of my understanding is incorrect.

Thanks!

(P.S. I saw a similar question being asked about

d(x^T)/dx

here Derivative of vector and vector transpose product, but it hasn't seem to be resolved.)

Result from matrix calculator: enter image description here

TShiong
  • 1,257
James Wang
  • 51
  • 2
    The calculator is correct. Hint: $\frac{\partial(x^T)}{\partial x}$ is the Jacobian of the function $(x_1,\dots,x_n)\mapsto (x_1,\dots,x_n),.$ – Kurt G. Sep 27 '23 at 06:25
  • 2
    It depends on the convention. I wouldn't call the calculator's result correct, but all of the entries are correct i.e. component wise the information is all the same as the correct answer. What your work hints at is that if we were careful about the distinction between contravariant and covariant indices, the result would be a type $(2,0)$ tensor (two covariant and no contravariant indices), but all matrices are type $(1,1)$ tensors (one of each) since that's how matrix multiplication works. – Ninad Munshi Sep 27 '23 at 07:05
  • Hi @Kurt, can you elaborate on your explanation? Shouldn’t it be the Jacobian of the function $(x_1,…,x_n)^T↦(x_1,…,x_n)$? I think the derivative in the problem should be a matrix-by-vector derivative (instead of vector-by-vector) - since $x$ and $x^T$ are different types of vectors, if one of them is defined to be a “vector”, the other cannot be considered (the same type) vector and can only be considered as a matrix. – James Wang Sep 27 '23 at 08:00
  • Nevertheless, I’m unsure of the correct approach to perform matrix-by-vector differentiation. – James Wang Sep 27 '23 at 08:06
  • In what sense differs my function from yours? The Jacobian of any function $f(x_1,\dots,x_n)$ is, as we know, the matrix $\frac{\partial f_i}{\partial x_j},.$ The usual convention is that $i$ is the row index. – Kurt G. Sep 27 '23 at 08:43

1 Answers1

2

$ \def\s{{\left(1\right)}} \def\t{\times} \def\o{{\tt1}} \def\n{n} $Treating this as the gradient of second-order tensors with dimensions $(\o\t\n)$ and $(\n\t\o)$ will work, and yields a fourth-order tensor with dimensions $(\o\t\n\t\n\t\o)$.

But why stop there? Everybody knows that third-order tensors are the true elements of reality. So this problem should be treated as the gradient of $(\o\t\n\t\o)$ by $(\n\t\o\t\o)$ tensors.

Then someone else will claim that third-order tensors are for amateurs and the REAL calculation should be done using fourth-order tensors, i.e. as the gradient of $(\o\t\n\t\o\t\o)$ by $(\n\t\o\t\o\t\o)$ quantities.

Ad infinitum.

The opposite approach is to eliminate all of the singleton dimensions and treat this as a simple vector-by-vector gradient, yielding the $(\n\t\n)$ identity matrix.

greg
  • 35,825