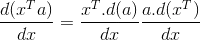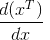14

I saw this answer here : Vector derivative w.r.t its transpose $\frac{d(Ax)}{d(x^T)}$.

enter image description here

I am finding difficult to understand the part in red. What rule is that ?

If I apply multiplication rule, shouldn't I get -

enter image description here

And how do one differentiate this anyways ?

enter image description here

Community
  • 1
Amit Tomar
  • 423

1 Answers1

30

You can do it componentwisely:

$$\frac{d(x^Ta)}{dx}=\left(\frac{d(x_1a_1+x_2a_2+\cdots+x_na_n)}{dx_1}, \frac{d(x_1a_1+x_2a_2+\cdots+x_na_n)}{dx_2}, \cdots, \frac{d(x_1a_1+x_2a_2+\cdots+x_na_n)}{dx_n}\right)\\ =(a_1,a_2,\cdots, a_n)=a^T$$

KittyL
  • 16,965
  • Aahh, din't realize it was that straightforward.. Thank you so much.. – Amit Tomar Jul 29 '15 at 10:46
  • This may be obvious, but if and are both vectors, then will be a scalar value, and so then wouldn't the derivative of a scalar value also be a scalar value? It feel strange that the derivative is a vector. – TheJKFever Apr 08 '20 at 03:17
  • @TheJKFever: Remember that you are looking for the derivative with respect to $x$. Ff $x$ is a vector, it includes derivative with respect to $x_1$, $x_2$, $\dots$, $x_n$, hence a vector. – KittyL Apr 09 '20 at 08:40