0

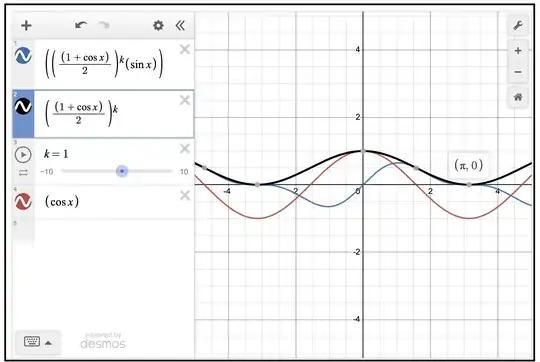
Can you please clarify how to prove this?

$$\int_{0}^{\pi}\left(\frac{1+\cos t}{2}\right)^{k}\operatorname{d}t>\int_{0}^{\pi}\left(\frac{1+\cos t}{2}\right)^{k}\sin t\operatorname{d}t$$

Here, $k=1,2,3,...$

This is from Section 4.24 in Rudin Real and Complex Analysis. This inequality is part of the proof to show that there is a trigonometric Polynomial approximation for all continuous complex periodic functions.

My question is about showing that the condition is greater than ">" as opposed to ">=".

I am able to plot these functions and sort of intuitively see this as shown below.

enter image description here

texmex
  • 800
  • I am confused because the question title shows a fslactor of $\cos x$ (or $\cos t$) in the greater quantity, but that factor does not appear in the question body. Please clarify/correct. – Oscar Lanzi Sep 22 '23 at 10:47
  • 2
    Why not $1>\sin x>0 \quad \Longrightarrow\quad \left(\frac{1+\cos x}{2}\right)^k > \left(\frac{1+\cos x}{2}\right)^k \sin x > 0$? – bFur4list Sep 22 '23 at 10:49
  • But sin $x = 0$ and sin $x = 1$ within the interval of integration right? – texmex Sep 22 '23 at 10:56
  • @OscarLanzi Please note I have corrected it to be "t" instead of "x". Thanks for pointing this out. – texmex Sep 22 '23 at 12:08

1 Answers1

2

note that if $f$ is continous on $[a,b]$ then the integral of f on the open interval $]a,b[$ have the same value of the integral on the closed interval $[a,b]$.You can see the the proof on this link Integrating on open vs. closed intervals .Regarding your question , $\forall x \in(0,\pi)$ , $0<sinx<1$, and $1+\cos(x)>0$ , so $\forall x \in(0,\pi),$ $(\frac{1+\cos(x)}{2})^k>(\frac{1+\cos(x)}{2})^k$$\sin(x)$ then $\int_{0}^{\pi}(\frac{1+\cos(x)}{2})^kdx>\int_{0}^{\pi}(\frac{1+\cos(x)}{2})^k\ sinxdx$

Mahmoud Mrowi
  • 360
  • Linking the related proof from this question about integration on open and closed intervals: https://math.stackexchange.com/questions/1980485/integrating-on-open-vs-closed-intervals – texmex Sep 22 '23 at 12:17
  • @texmex Thanks for the warning, I will post it – Mahmoud Mrowi Sep 22 '23 at 12:55