Energy minimization doesn't seem to yield a geodesic

Question

I'm minimizing (through optimization using gradient descent) the energy $E(\gamma)=\int_{t_1}^{t_2} g_{\alpha\beta}(\gamma^{\alpha})'(\gamma^{\beta})'\operatorname{d}\!t$ of a curve using the inner product induced by the metric tensor. In my case the metric tensor is from information geometry (the Fisher metric) which is very simple for a univariate gaussian.

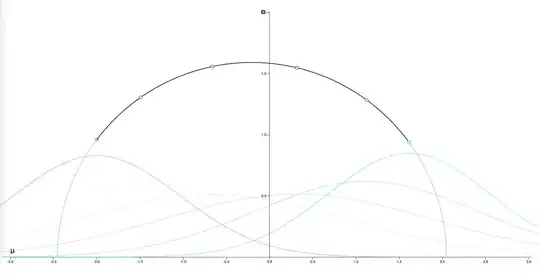
However, given that I'm using the Fisher metric as the metric tensor, I would expect that a geodesic of a univariate gaussian to follow an arc (e.g. shortest path between two univariate gaussian distributions is not a straight line as shown here). However, after optimizing the curve to minimize the energy, I'm always getting a straight line as distance between two univariate gaussians (using the same start/end points of the linked article from geomstats). Am I missing something ?

More details: I'm using a parametrized cubic spline curve (just as in here), just to give more details about which curve I'm using.

Trying to make the question more simple

I'm using the following metric (the Fisher metric as linked above) for computing the inner products:

$[ 1/scale, 2/scale ]$ (the matrix is 2x2, this is the diagonal, other elements are zero)

I have 2 parameters (mean, scale), and as you can see, the metric depends only on the scale. These parameters are parametrizing a univariate gaussian distribution (w/ mean and scale), and it is known that this metric induces an hyperbolic geometry (you can understand this better by looking at this animation, just click and drag and you will see the curve geodesic in the parameter space).

(note that y is my scale and x is mean, the dark black arc line is the geodesic, but this is not what I'm getting)

Now, if I minimize $E(\gamma)$ (using gradient descent) to optimize the curve parameters, what I get is a straight line connecting the parameters in the parameter space, while I would expect it to be curved as induced by the metric tensor.

Answer 1

I assume scale is the variance.

You have the metric wrong: it should have been $\text{diag}(1/\nu, 1/2\nu^2)$ where $\nu$ is the scale/variance, ie $$ g_{\mu\mu}=\frac{1}{\nu},\; g_{\mu\nu}=0,\; g_{\nu\nu}=\frac{1}{2\nu^2}. $$

That said, I suspect you might also have some problem with finding the geodesics as the $\text{diag}(1/\nu, 2/\nu)$ metric should not result in horizontal lines being geodesic.

A last thing, I suspect that in order to get half-circles as geodesics, you need to use parameters $(\mu,\sigma)$, ie standard deviation instead of scale/variance.

Answer 2

By definition, geodesic can be defined through minimization of the following functional, $$L=\int_{0}^{1}dt\,\sqrt{g_{ij}(t)\dot{\xi}^i(t)\dot{\xi}^j(t)}$$ and the resulting equation for geodesic is $$\ddot{\xi}^i(t)+\Gamma_{jk}^i\dot{\xi}^j(t)\dot{\xi}^k(t)=0.$$ Gaussian statistical manifold has the following metric, $$g_{ij}=\frac{1}{\sigma^2}\begin{pmatrix}1 & 0 \\ 0 & 2\end{pmatrix}.$$ I have forget that one can also derive the geodesic equation from the energy functional (see related questions and answers below). Let me denote that $\mu$ corresponds to index $1$ and $\sigma$ corresponds to index $2$. Non-zero Christoffel symbols are $$\Gamma_{11}^{2}=\frac{1}{2\sigma},\,\Gamma_{12}^{1}=-\frac{1}{\sigma},\,\Gamma_{22}^{2}=-\frac{1}{\sigma}.$$ Equations for geodesic become $$\frac{d^2\mu}{ds^2}-\frac{2}{\sigma}\frac{d\mu}{ds}\frac{d\sigma}{ds}=0, \frac{d^2\sigma}{ds^2}+\frac{1}{2\sigma}\left(\frac{d\mu}{ds}\right)^2-\left(\frac{d\sigma}{ds}\right)^2=0.$$ After some derivations, I find $$\pm d\mu=\pm\frac{A\sqrt{2}\sigma\,d\sigma}{\sqrt{1-A^2\sigma^2}}.$$ Integrating both sides, I finally write $$\pm \mu \pm A\sqrt{2}\int\frac{d\sigma\,\sigma}{\sqrt{1-A^2\sigma^2}}=B,$$ where $A$ and $B$ are some constants. Further integration is easy and then you can check that this equation defines the arc (or vertical line) in $(\mu,\sigma)$-plane.

Some fun: one can consider the gradient flow on Guassian statistical manifold, $$\frac{d\theta}{dt}=-g^{-1}\frac{\partial\psi(\theta)}{\partial\theta},$$ where $\theta=(\theta_1,\theta_2)$, $\theta_1=\mu/\sigma^2$, $\theta_2=-(2\sigma)^{-2}$ are so-called canonical variables and $\psi(\theta)=\mu^2/(2\sigma^2)+\ln(\sigma\sqrt{2\pi})$ is potential function. Here $g$ denotes metric in $(\theta_1,\theta_2)$ variables and $g^{-1}$ corresponds to inverse metric. This gradient flow can be associated with dynamical system (in left hand side we haver derivatives, $\dot{\theta}_1$ & $\dot{\theta}_2$). It is funny that the following function $$H=\frac{1}{\theta_1}+\frac{\theta_1}{2\theta_2}$$ can be considered as integral of motion, roughly speaking "Hamiltonian". If one represents $H=PQ$, where $P$ and $Q$ are canonical variables in Hamilton mechanics sense, the system reduces to $$\dot{Q}=-\frac{\partial H}{\partial P},\,\dot{P}=+\frac{\partial H}{\partial Q}.$$ In $(\mu,\sigma)$-variables, we have $$\dot{\mu}=-\mu,\quad \dot{\sigma}=-\frac{\sigma^2+\mu^2}{2\sigma}$$ and it defines a family of arcs, parametrized by $H$, $$\left(\mu(t)-\frac{H}{2}\right)^2+\sigma(t)^2=\left(\frac{H}{2}\right)^2.$$

To sum up,

1. Is the energy function at the very first line in you question correct? May be square root is missed?
2. Gaussian distribution is the exponential distribution and its metric can be computed as Hessian of potential function. You can consider the gradient flow of potential function in order to proove that geodesics are arcs.
3. Naively, I do not see the problem with trappin in local minima. It seems that double check of the code is needed.

References:

1. "Information geometry and its applications", S. Amari
2. "On Finding Geodesic Equation of Normal Distribution and Gaussian Curvature", Willian W. S.Chen, 10.4236/am.2017.89098
3. "Completely integrable gradient systems on the manifolds of Gaussian and multinomial distributions", Y. Nakamura, 10.1007/BF03167571

May be helpful:

1. Critical curves of energy functional
2. Finsler geodesic equations

P.S.: how we can help you, if you compute everything numerically and provides only pieces of expressions?