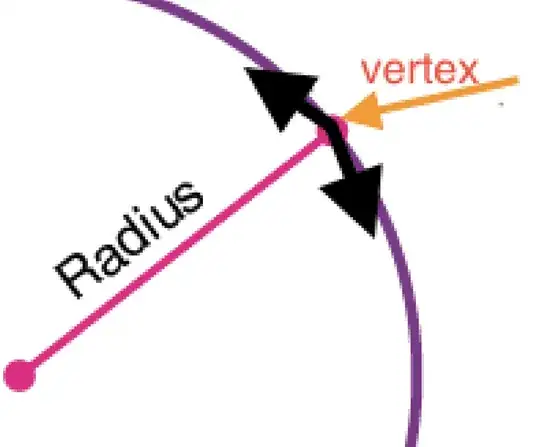
A vertex is defined as a 'meeting point of two lines that form an angle'.
When I increment the circumference of a circle into infinitesimal small increments I get something like shown below in the picture.
This infinitesimal small increment of the circumference can then be divided into left and right which is shown by the black arrows in the picture.
My question is, if the part of the circumference is infinitesimal small, the left and right part of it would not be curved and therefor the above mentioned description of a vertex would be true.