Conjecture about the mean value of an almost periodic function (the "Mountains of Guilin")

Question

Consider the function $f_{p_j,n}(x)=|\sin (p_1x)+\sin (p_2x)+\dots+\sin (p_nx)|$ where $p_j$ is any sequence such that no two $p$ are rational multiples of each other where the $p_j$ are linearly independent over $\mathbb{Q}$ (so the function is almost periodic). (After reading @mollyerin's answer, I changed the condition on $p_j$.)

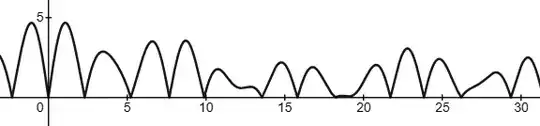
For example, here is the graph of $f_{2^{1/j},\color{red}{5}}(x)$ :

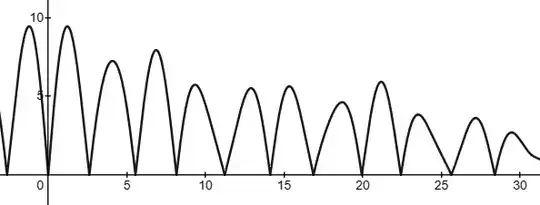
And here is the graph of $f_{2^{1/j},\color{red}{10}}(x)$ :

I call this kind of function $f_{p_j,n}(x)$, the "Mountains of Guilin".

Now consider the mean value of $f_{p_j,n}(x)$. I have evidence that suggests that:

• For any given value of $n$, the mean value of $f_{p_j,n}(x)$ is independent of the choice of sequence $p_j$ (as long as the $p_j$ are linearly independent over $\mathbb{Q}$).
• The mean value of $f_{p_j,\color{red}{2}}(x)$ is $8/\pi^2$.

I have not been able to find a general expression for the mean value of $f_{p_j,n}(x)$ in terms of $n$, but I have the following conjecture:

$$\color{red}{\lim_{n\to\infty}\frac{\text{mean value of $f_{p_j,n}(x)$}}{\sqrt n}=\frac{1}{\sqrt \pi}}$$

Is my conjecture true?

Numerical evidence for my conjecture:

Using desmos, I approximated the mean value of $f_{2^{1/j},n}(x)$ as $M_n=\frac{1}{10^7}\sum\limits_{k=1}^{10^7}|\sin (2^1k)+\sin (2^{1/2}k)+\dots+\sin (2^{1/n}k)|$

Letting $L(n)=\dfrac{M_n}{\sqrt n}$, we have:

$L(1)\approx 1.128379\left(\frac{1}{\sqrt \pi}\right)$
$L(2)\approx 1.015898\left(\frac{1}{\sqrt \pi}\right)$
$L(10)\approx 1.006373\left(\frac{1}{\sqrt \pi}\right)$
$L(100)\approx 1.000334\left(\frac{1}{\sqrt \pi}\right)$

This suggests that my conjecture may be true, but I don't know how to prove it.

Visual representation of the mean value:

If my conjecture is true, then there is a nice way to visually represent the mean value of the function. Draw a circle of area $n$ with its centre on the $x$-axis. A horizontal line through the top of the circle represents, approximately, the average value of the function.

Answer 1

Here is a non-rigorous argument that the conjecture is true:

Let $\phi_t$ be the flow on $\mathbb{T}^n = \mathbb{R}^n / (2 \pi \mathbb{Z}^n)$ given by $(x_1, \dots, x_n) \mapsto (x_1 + p_1 t, \dots, x_n + p_n t)$. By your assumptions on $p_i$, this flow should be uniquely ergodic. (The standard argument is: the closure of the subgroup $\langle \phi_t \rangle$ of $\mathbb{T}^n$ generated by $\phi_t$ is all of $\mathbb{T}^n$, so any measure invariant under $\phi_t$ is invariant under $\mathbb{T}_n$, but Haar measure on $\mathbb{T}_n$ is unique up to scaling.)

[Edit: In fact I think to apply the above you need the $p_i$ to be linearly independent over $\mathbb{Q}$, rather than just pairwise so. For instance, with $p_1, p_2, p_3 = 1, \pi, 1+\pi$, on the torus your flow remains in the plane $z = x + y$ (or a plane parallel to that), so reductions to integrals over all of $\mathbb{T}^n$ don't follow.]

Write $f(x) = \sum \sin(x_i p_i)$. It follows from unique ergodicity (and maybe you also need the Birkhoff ergodic theorem) that for any $x \in \mathbb{T}^n$ $$ \lim_{T \to \infty} \frac{1}{T} \int_0^T |f(\phi_t x)| dt= \int_{\mathbb{T}^n} |f(x)| d\mu, $$ where $\mu$ is the standard probability measure on our torus (it's $1/(2\pi)^n$ times Lebesgue measure given our identifications).

So it is enough to estimate the integral $$ \frac{1}{(2\pi)^n} \int_{[0, 2\pi]^n} \Big| \sum \sin(x_i) \Big| dx_1 \cdots dx_n. $$ To do this, use the central limit theorem. On $[0, 2\pi]$, $\sin(x)$ has mean $0$ and standard deviation $1/\sqrt{2}$, so CLT tells us $$ \frac{1}{\sqrt{n}} \sum \sin(x_i) \sim \mathcal{N}\Big(0, \frac{1}{\sqrt{2}} \Big). $$ So estimating $\sum |\sin(x_i)|$ is computing the expected value of $|x|$ on the normal distribution with standard deviation $\sqrt{n/2}$. One computes in general that $$ \frac{1}{\sigma \sqrt{2 \pi}} \int_{-\infty}^{\infty} |x| e^{-x^2/2\sigma^2} dx = \frac{2}{\sigma \sqrt{2 \pi}} \int_{0}^{\infty} x e^{-x^2/2\sigma^2} dx = \frac{\sigma}{\sqrt{2\pi}}. $$ Plugging in $\sigma = \sqrt{n/2}$, one gets the estimate $$ \frac{1}{(2\pi)^n} \int_{[0, 2\pi]^n} \Big| \sum \sin(x_i) \Big| dx_1 \cdots dx_n \approx \sqrt{\frac{n}{\pi}}. $$