1

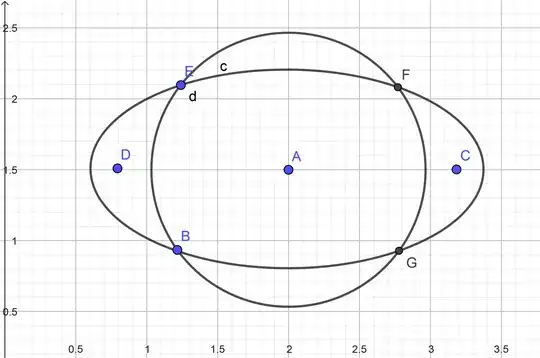
I have a circle and an ellipse with the following general equations:

\begin{align*} Circle: (x - m)^2 + (y - n)^2 &= r^2 \\\ Ellipse: \frac{(x - o)^2}{a^2} + \frac{(y - p)^2}{b^2} &= 1 \end{align*}

Where $(x, y)$ are coordinates for the intersection point(s), $(m, n)$ is the center of the circle, $r$ is the circle's radius, $(o, p)$ is the center of the ellipse, $a$ is major radius and $b$ is minor radius. The ellipse has inclination of $0^\circ$.

Obviously I know every value except $(x, y)$ so I can opt for a numerical solution but that's not what I need.

I know that there are 6 cases for the solution depending on the number of intersection points:

  • no points
  • 1 (sharing a tangent line)
  • 2
  • 3 (one point sharing a tangent line)
  • 4
  • infinitely many (if centers and radii are the same)

I've looked at other questions but they are using other equations like that one or are asking for the area of the intersection like that one.

If you cannot provide the equations, at least some pointers on how to solve this would be appreciated.

sanitizedUser
  • 135
  • Please also refer to comments from another post here. – Ng Chung Tak Jul 16 '23 at 08:02
  • 1
    Do you want to classify all the possible solutions? Is that a useful thing to do? – Paul Jul 16 '23 at 08:54
  • 1
    $3$ common points are also possible, one of them being a point of tangency. – user376343 Jul 16 '23 at 11:55
  • @Paul What do you mean? I need to know how many solutions there are in the real 2D plane and what their coordinates are. The complex solutions are not interesting to me. – sanitizedUser Jul 16 '23 at 12:38
  • The system of two given equations leads to two functions $$x=f_1(a,b,m,n,r,o,p)\y=f_2(a,b,m,n,r,o,p)$$ and all statement about the intersection points is coming from these two functions (the form of these functions is certainly not rational). – Piquito Jul 17 '23 at 21:51

1 Answers1

0

enter image description here

Comment: As shown in picture for each point of intersection, we must have a system of two equations of first degree $C(x.y)=c$ which represent the circle and $E(x, y)=e $ which represents the ellipse. These equations are resulting from factorization of equations of circle and ellipse to first degree factors. Suppose we get :

$Circle: C(x, y)=c_1\cdot c_2$

and from ellipse:

$Ellipse: E(x, y))=e_1\cdot e_2$

then we have to search for solution of following system of equations of first degree:

$\begin{cases}C(x, y)=c_1\\E(x, y)=e_1\end{cases}$

$\begin{cases}C(x, y)=c_1\\E(x, y)=e_2\end{cases}$

$\begin{cases}C(x, y)=c_2\\E(x, y)=e_1\end{cases}$

$\begin{cases}C(x, y)=c_2\\E(x, y)=e_2\end{cases}$

which give the coordinates of points E, F, G and B, in case they intersect. You may find one, two, three or four solutions or nothing at all(when all systems are inconsistent).

Note:

A similar question I answered long ago but I could not find it. You can also that if you find.

sirous
  • 10,751