5

I used the equations found on Paul Bourke's "Circles and spheres" page to calculate the intersection points of two circles:

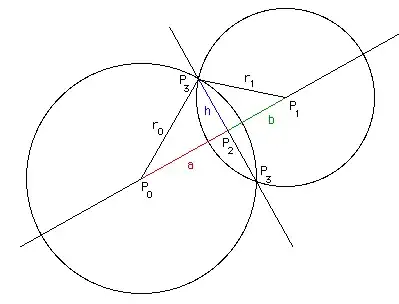
Image of intersecting circles from Paul Bourke's page

$P_3$ is what I'm trying to get, except now I want to do the same with two ellipses.

Calculating $h$ is the tricky bit. With regular circles, it can be done with the Pythagorean Theorem $a^2 + b^2 = c^2$, since we already know $r_0$ (the radius): $$h = \sqrt{a^2 + r_0^2}.$$

With ellipses it seems much trickier. I don't know how to calculate $h$. There is not a single radius anymore: there are $\operatorname{radiusX}$ and $\operatorname{radiusY}$.

Given $\operatorname{radiusX}$, $\operatorname{radiusY}$, and the center points $(x,y)$ of each ellipse, how do I find the two intersecting points? (Note: the ellipses are guaranteed to have two intersecting points in my specific application.)

user642796
  • 52,188
999
  • 151
  • 3
    Should this not be a question for the Mathematics forum instead? –  Jan 27 '12 at 11:40
  • 2
    I don't understand - are the ellipses alligned, sharing a major axis? – hugomg Jan 27 '12 at 11:40
  • Are the ellipse rotated? Have you considered the following equation of the ellipse sqr((cx-x)/radiusX) + sqr((cy-y)/radiusY) = 1.0 ? starting with this equation should help you find the solution right? –  Jan 27 '12 at 11:42
  • 1
    Have you seen these solutions? http://www.analyzemath.com/EllipseProblems/ellipse_intersection.html http://mathforum.org/library/drmath/view/66877.html http://www.math.niu.edu/~rusin/known-math/99/2ellipses –  Jan 27 '12 at 11:42

3 Answers3

3

Two ellipses can intersect in up to $4$ points. The system of two equations in two variables is equivalent to solving one polynomial of degree $4$ in one variable. In your case it is known that two of the solutions of this polynomial are real, but this does not simplify anything algebraically except for a few cases where there is some special geometric relationship between the ellipses. An exact solution in terms of the equations defining the ellipses will have the same complicated zoo of nested radicals as the formula for solving a general quartic equation. Unless for some unusual reason you really need the infinite-precision algebraic answer, it is simpler to solve numerically for the two intersection points.

zyx
  • 35,436
  • This is pretty much the answer I was coming back to make. Years ago I know someone who worked out a general solution - it was full of special cases and I think had to deal with 2, 3, 4 intersection points separately. If this is to solve a practical problem you are better off using a numeric technique to home in on the solutions. – half-integer fan Mar 06 '13 at 22:41
2

You should use conic sections. Say C1 is conic section of first ellipse and C2 is conic section of second ellipse. Then if C1 and C2 intersect then also their linear combination C3=C1+t.C2 must be intersecting. Choose t so that C3 is degenerate, that means det(C3)=0. This determinant leads to cubic equation for t. So you get up to 3 values of t. For each t evaluate C3. Since C3 is degenerate, it represents system of two lines (they can be equal). Calculate intersection of both lines with first ellipse and test if the intersection point is on second ellipse. This will give you all intersection points of the two ellipses (some results may be duplicated, but this should be easy to detect and avoid).

BTW, to simplify algebra, it is good idea to transform first ellipses so that one of them is in origin with axis on cartesian axis. Such ellipse is then x^2/a^2 + y^2/b^2 = 1 and conic section is very simple:

(b^2, 0, 0)
(0, a^2, 0)
(0, 0, -a^2.b^2)
1

Let your ellipses has their foci on X-axis. Then calculate points of intersection of both ellipses by solving the system:

x^2/a1 + y^2/b1 = 1

and

x^2/a2 + y^2/b2 = 1

h will be a Y and -Y of this two point of solution.