How could we define circulation over a surface or a tangential surface integral?

Question

The definition of surface integral of a vector function is about the projection of a function on the normal vector, so it is impossible for tangential vector fields to be intergrated over a surface, for the integral would be always zero. I would like to extend this thought as follows: I found this definition of $curl$ of a vector field: $$(\nabla \times \mathbf F)(p):=\lim_{V\to 0} \frac {1}{|V|} \oint_S \mathbf n \times \mathbf F dS, $$ where $p$ is a point inside a volume $V$ with boundary the surface $S$. The vector $\mathbf n \times \mathbf F$ is in fact tangential to the surface, and it sounds nice to integrate over the surface to find the given total rate. But I cannot understand the exact meaning of this "integral". I would like to ask: How could we present the circulation over $a$ $surface$ -and not over a curve?

Answer 1

I will suggest an approach. Let $S$ a parametrized smooth surface of $\mathbb R^3$ and $\mathbf F:S\to \mathbb R^3$ a vector field. We also define the outer normal unit vector field of $S$ as $\mathbf n:S\to \mathbb R^3$ such that $\forall \mathbf p\in S : \mathbf n(\mathbf p)\bot \Pi_S(\mathbf p)$, where $\Pi_S(\mathbf p)$ is considered as the tangent plane of $S$ at $\mathbf p$. Let $\mathbf p\in S$. We clearly observe that vector $\mathbf F(\mathbf p)-(\mathbf F(\mathbf p)\cdot \mathbf n(\mathbf p))\mathbf n(\mathbf p)$ belongs to $\Pi_S(\mathbf p)$, thus it is tangential to $S$ at $\mathbf p$, and moreover it is the projection of our vector field on $\Pi_S$. Set $\mathbf t(\mathbf p)$ the normalized above tangent vector. By analogy with the common surface integral $\int_S \mathbf F\cdot d\mathbf S=\int_S \mathbf F\cdot \mathbf ndS$, we introduce $$\int_S \mathbf F\cdot d\mathbf S_t=\int_S \mathbf F \cdot \mathbf t dS,$$ where the last expression equals to $$\int_D (\mathbf F\cdot \mathbf t)(\mathbf Σ(u,v))|(\mathbf Σ_u\times\mathbf Σ_v)(u,v)|dudv,$$ which is of course a double integral over the parametric region of $\mathbf Σ$.

In order to avoid the above expression of $\mathbf t$ and introduce a more compact one, we could define it as $$\mathbf t:=-\frac {\mathbf n \times(\mathbf n\times \mathbf F)}{|\mathbf n \times(\mathbf n\times \mathbf F)|},$$ thus $$\int_S \mathbf F\cdot \mathbf t dS=-\int_S \mathbf F \cdot \frac {\mathbf n \times(\mathbf n\times \mathbf F)}{|\mathbf n \times(\mathbf n\times \mathbf F)|} dS=\int_S (-\mathbf n \times \mathbf F)\cdot \frac {\mathbf F \times \mathbf n}{|\mathbf n \times(\mathbf n\times \mathbf F)|} dS=\int_S \frac {|\mathbf F \times \mathbf n|^2}{|\mathbf n \times(\mathbf n\times \mathbf F)|} dS=\int_S \frac {|\mathbf F \times \mathbf n|^2}{|\mathbf n\times \mathbf F|}dS=\int_S |\mathbf F \times \mathbf n|dS=\int_S |\mathbf F \times \mathbf d\mathbf S|,$$

where $d\mathbf S=\mathbf n dS$, as usual.

I think that this is a good attempt for "overall tangential contribution" of $\mathbf F$ on $S$, but I am not conclusively convinced about that.

Answer 2

That "geometric" definition of curl can be found in [1] on p. 398 but they do not seem to prove it. It follows from the following

Claim. For any volume $V$ that is bounded by the closed surface $S$ and a differentiable vector field $\boldsymbol{F}$ we have $$\tag{1} \int_V\nabla\times \boldsymbol{F}\,dV=\oint_S\boldsymbol{n}\times \boldsymbol{F}\,dS $$ where $\boldsymbol{n}$ is the unit normal at the surface.

Proof. Componentwise eq. (1) reads as \begin{align} \tag{2}\int_V\partial_2F_3-\partial_3F_2\,dV&=\oint_Sn_2F_3-n_3F_2\,dS\,,\\ \tag{3}\int_V\partial_3F_1-\partial_1F_3\,dV&=\oint_Sn_3F_1-n_1F_3\,dS\,,\\ \tag{4}\int_V\partial_1F_2-\partial_2F_1\,dV&=\oint_Sn_1F_2-n_2F_1\,dS\,. \end{align} Each of these equations follows directly from Gauss' divergence theorem applied to the vector fields $$ \begin{pmatrix} 0\\ F_3\\-F_2\end{pmatrix}\,,\quad \begin{pmatrix} -F_3\\ 0\\F_1\end{pmatrix}\,,\quad \begin{pmatrix} F_2\\ -F_1\\0\end{pmatrix}\,,\quad $$ respectively. $$\tag*{$\Box$} \quad $$

To answer your question about a surface integral of tangential component of a vector field:

• The RHS in (1) is a vector of ordinary surface integrals each of which contains the dot product of a vector field with the normal to the surface.

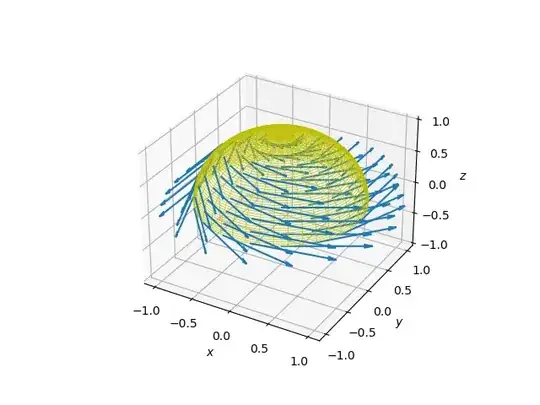
• Alternatively one can view the RHS of, say, (4) as the dot product $\boldsymbol{t}\cdot\boldsymbol{F}$ where $$\tag{5} \boldsymbol{t}=\begin{pmatrix}-n_2\\n_1\\0\end{pmatrix}\,. $$ This is a vector field tangential to the surface. See image below.

• For a unit sphere the unit normal is $$ \begin{pmatrix}x\\y\\z\end{pmatrix} $$ and therefore the tangential field (5) is $$ \boldsymbol{t}=\begin{pmatrix}-y\\x\\0\end{pmatrix}\,. $$ Its curl is constant and points along the $z$-axis: $$ \nabla\times \boldsymbol{t}=\begin{pmatrix}2\\0\\0\end{pmatrix}\,. $$

• It should be intuitively clear that the $z$-component of the curl of $\mathbf{F}$ is the surface integral (4) of the dot product $\boldsymbol{t}\cdot\boldsymbol{F}\,.$ The same reasoning applies to (2) and (3).

Image of the tangential field $\boldsymbol{t}\,:$

[1] K.F. Riley, M.P. Hobson, S.J. Bence, Mathematical Methods for Physics and Engineering.