Consider the inverse Mellin transform of the function $(ix)^{-s}$ for $x>0$. This is: $$ \frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty} (i x)^{-s} ds $$ What does this evaluate to? I believe that if you simply had $x^{-s}$ then the result would be $\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty} x^{-s} ds = \delta(x-1)$. However what happens in this case where there a factor of $i$?
-
3If $\frac1{2\pi i}\int_{c-i\infty}^{c+i\infty} y^{-s}ds=\delta(y-1)$ and $y=ix$, then the answer is $\delta(i x-1)$. Look for sources like Delta function of imaginary argument. Right? – Тyma Gaidash Jul 11 '23 at 15:30
-
1@TymaGaidash I don't think this works since $\delta(i x-1)$ in the integrand of the Mellin transform $\int\limits_0^\infty \delta(i x-1), x^{s-1}, dx$ is undefined for $x\in\mathbb{R}$ except at $x=0$ where it evaluates to $0$. – Steven Clark Jul 14 '23 at 21:57
2 Answers
I don't believe the inverse Mellin transform of $i^{-s}$ converges, but one can approximate the inverse Mellin transform of $i^{-s}$ as
$$f(x)=\mathcal{M}_s^{-1}\left[i^{-s}\right](x)=\underset{T\to\infty}{\text{lim}}\left(\frac{1}{2 \pi i}\int\limits_{c-i T}^{c+i T} i^{-s}\, x^{-s} \, ds\right)$$ $$=\underset{T\to \infty }{\text{lim}}\left(\frac{e^{-\frac{1}{2} \pi (T+i c)} \left(e^{\pi T}-x^{2 i T}\right) x^{-c-i T}}{\pi (\pi -2 i \log (x))}\right)\tag{1}.$$
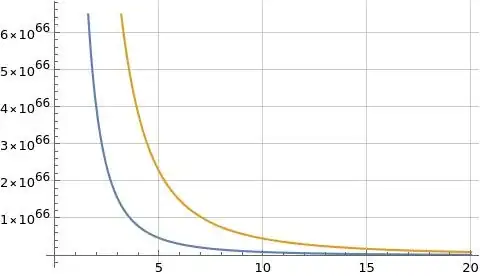
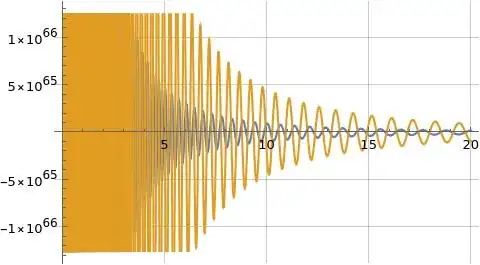
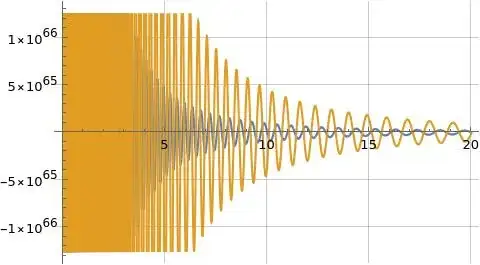
Figures (1) to (3) below illustrate $|f(x)|$, $\Re(f(x))$, and $\Im(f(x))$ where formula (1) is evaluated with $T=100$ and $T=101$ in blue and orange respectively where in all cases the value $c=2$ was used to evaluate formula (1). I believe $c=2$ is a valid choice since the function $i^{-s}$ is analytic for $s\in\mathbb{C}$. Note formula (1) for $f(x)$ seems to diverge significantly in magnitude as $T$ increases.
Figure (1): Illustration of $|f(x)|$ with $T=100$ (blue) and $T=101$ (orange)
Figure (2): Illustration of $\Re(f(x))$ with $T=100$ (blue) and $T=101$ (orange)
Figure (3): Illustration of $\Im(f(x))$ with $T=100$ (blue) and $T=101$ (orange)
I'll also note the frequency of the oscillations in $\Re(f(x))$ and $\Im(f(x))$ also seem to diverge (increase) as $T$ increases, but this is perhaps not as noticeable in Figures (1) to (3) above. This is because $T=100$ and $T=101$ are very close in magnitude and the frequency oscillation doesn't seem to diverge as rapidly as the magnitude as $T$ increases.
- 7,363
I start by saying that, in the developments below
- I follow the path described by @TymaGaidash in their comment to the OP.
- I approach the problem by using reference [1], precisely example 11.2.7 in chapter 11 "The Mellin Transform" by Jacqueline Bertrand, Pierre Bertrand and Jean-Philippe Orvalez: however the development is not the same.
- I use the "function" notation for distributions, i.e. I'll write $f(x)$ instead of $\langle f,\varphi\rangle$ for $\varphi \in C^\infty_0(\Bbb R^n)$ and thus I'll write $$\DeclareMathOperator{\Dd}{d\!} \delta(x-x_0)=\frac{1}{2\pi}\int\limits_{-\infty}^{+\infty} e^{-i\omega(x-x_0)} \Dd\omega\label{1}\tag{1} $$ and moreover, for the change of variable formula in the theory of distributions I refer to this old answer of mine and to the references cited there.
The inverse Mellin transform of $i^{-s}$, $s\in \Bbb C$ is $$ \begin{split} f(x) = \mathscr{M}^{-1} [\varphi(s)]( x) & = \frac{1}{2\pi i}\int\limits_{c-i\infty}^{c+i\infty} \varphi(s)x^{-s} \Dd s =\frac{1}{2\pi i}\int\limits_{c-i\infty}^{c+i\infty} (ix)^{-s} \Dd s = \frac{1}{2\pi i}\int\limits_{-i\infty}^{+i\infty} ({x}{i})^{-s} \Dd s\\ &\text{(the choice $c=0$ is allowed by the holomorphy $(ix)^{-s}$}\\ &\text{in the whole $s$-plane, and thus by putting $s=i\omega$ we get)} \\ & = \frac{1}{2\pi}\int\limits_{-\infty}^{+\infty} e^{-i\omega \ln({x}{i})} \Dd \omega = \frac{1}{2\pi}\int\limits_{-\infty}^{+\infty} e^{-i\omega (\ln x+ \ln i)} \Dd \omega\\ &\text{(and finally, by identity \eqref{1}, and by the standard}\\ &\text{change of variable formula for distributions)}\\ & = \delta (\ln x+\ln i)=\delta \left(\ln({x}{i})\right)= \delta (x+i) \end{split} $$ By using the change of variable formula, it can be easily seen that $\delta(x+i)=\delta(ix-1)$ which is the form considered in the comments to the OP.
Interpretation of the result.
As we have seen, the inverse Mellin transform of $\varphi(s)=i^{-s}$ can be explicitly calculated and has the value already given in the comments above. And as @StevenClark points out in his comment to the OP, the result implies that $i^{-s}$ is not the Mellin transform of any function/distribution supported on the non negative real axis $\Bbb R_{\ge0}=\{x\in \Bbb R : x\ge 0\}$, i.e.
$$
0=\int\limits_{0}^{+\infty} \delta(x+i) x^{s-1} \Dd x \neq \mathscr{M} [f(x)](s) \quad\text{ for any }f\in\mathscr{D}^\prime(\Bbb R_{\ge0})
$$
However note that $\delta(x+i)\in \mathscr{D}^\prime(\Bbb C)$ and this is the key to understand the problem: the standard Mellin transform maps a function/distribution supported on the positive semi-axis to a function/distribution supported in a complex semi-plane. If the support has an empty intersection with $\Bbb R_{\ge0}$, then the transformed function is always $0$.
Nevertheless a similar problem has been solved for the Laplace transform and gave rise to the so called (generalized Borel-)Laplace transform (see [2]): the solution consists precisely in defining the transform on a rotated semi-axis in $\Bbb C$ in order to have a non empty intersection between the support of the transform and the support of the function/distribution to be transformed: in the case at hand, if we define the generalied Mellin transform as
$$
\color{blue}{
{^{\pi/2}\!\!\mathscr{M}} [f(x)](s)= \!\!\! \!\!\! \int\limits_{0}^{\quad\infty e^{i\frac{\pi}{2}}}\!\!\! f(x) x^{s-1} \Dd x }
$$
where $[0,\infty e^{i\frac{\pi}{2}}[$ is the upper imaginary axis in $\Bbb C$ i.e. $\{z\in \Bbb C: \Re{z}=0 \wedge \Im{z}=\pi/2\}$, we have that
$$
\color{green}{
\begin{split}
{^{\pi/2}\!\!\mathscr{M}} [\delta(x+i)](s) &= \!\!\! \!\!\! \int\limits_{0}^{\quad \infty e^{i\frac{\pi}{2}}} \!\!\! \delta(x+i) x^{s-1} \Dd x \\
&\text{and thus by putting $\xi=ix$ we get)} \\
& = i^{-1}\int\limits_{0}^{+\infty } \delta(-i\xi+i)(-i\xi)^{s-1} \Dd \xi \\
& = i^{-1} (-i)^{s-1} =i^{-1} \left(\frac{1}{i}\right)^{s-1} = i^{-1} (i)^{1-s} = i^{-s}
\end{split}}
$$
thus we have reestablished a duality between the (generalized) Mellin transform and its (standard) inverse transform.
In sum it is correct to say that $i^{-s}$ is the Mellin image of the distribution $\delta(x+i)$ provided the generalized Mellin transform is considered instead of the standard one.
References
[1] Alexander D. Poularikas (ed.), The transforms and applications handbook, (English) The Electrical Engineering Handbook Series. Aylesfort: CRC Press. New York, NY: IEEE Press, pp. vii+1103 (1996), ISBN:0-8493-8342-0, MR1407750, Zbl 0851.44001.
[2] Boris Yu. Sternin, Victor Shatalov, Borel-Laplace transform and asymptotic theory. Introduction to resurgent analysis, Boca Raton, FL: CRC Press. pp. 270 (1996), Zbl 0852.34001.
- 9,727
-
But in your integral $i^{-1} \int\limits_0^{\infty} \delta(-i \xi+i), (-i \xi)^{s-1} , d\xi$, the Dirac delta function $\delta(-i \xi+i)$ is still undefined for $\xi\in\mathbb{R}$. On the other hand, $\int\limits_0^{-i \infty} \delta(i x-1), x^{s-1} , dx\overset{{x\to -i \xi}}{=}\int\limits_0^{\infty} \delta(\xi-1), (-i \xi)^{s-1} (-i) , d\xi=(-i)^s=i^{-s}$. – Steven Clark Jul 17 '23 at 17:52
-
Using the Dirac delta representation $\delta(x)=\underset{T\to \infty}{\text{lim}}\left(\frac{1}{2 \pi} \int\limits_{-T}^T e^{-i x \omega} , d\omega\right)=\underset{T\to \infty}{\text{lim}}\left(\frac{\sin(T x)}{\pi x}\right)$, note that $\int\limits_0^{\infty} \frac{\sin(T, (\xi-1))}{\pi (\xi-1)} , d\xi=\frac{\text{Si}(T)}{\pi}+\frac{1}{2}$ and $\underset{T\to\infty}{\text{lim}}\left(\frac{\text{Si}(T)}{\pi}+\frac{1}{2}\right)=1$, whereas the integral $\int\limits_0^{\infty} \frac{\sin(T, (-i \xi+i))}{\pi (-i \xi+i)} , d\xi$ doesn't converge. – Steven Clark Jul 17 '23 at 18:00
-
@StevenClark, about your first comment, no $\delta(-i\xi+i)$ is correctly defined for $\xi\in\Bbb R$ since it is $\delta\big(i(-\xi+1)\big)$ an note that when $\xi=1\in\Bbb R$ you have correctly $\delta\big(i(-\xi+1)\big)=\delta (0)$. – Daniele Tampieri Jul 17 '23 at 18:06
-
An integral of the Dirac delta function only makes sense when it can be mapped to an integral where both the argument of the Dirac delta function and the integration range are real. In your integral the integration range is real, but the argument is imaginary except at $\xi=1$. Your integral diverges as noted in my second comment above. – Steven Clark Jul 17 '23 at 18:06
-
See WolframAlpha evaluation of $\int\limits\limits_0^{\infty} \delta(-i \xi+i) , d\xi$. – Steven Clark Jul 17 '23 at 18:16
-
@StevenClark, as I said $\delta(x+i)\in\mathscr{D}^\prime(\Bbb C)$ – Daniele Tampieri Jul 17 '23 at 18:17
-
Perhaps I'm a bit confused, but in my second comment above I used the Dirac delta function defined in formula (1) of your answer above to make my point that your integral diverges. Are you redefining the Dirac delta function? Also, what is wrong with last formula in my original comment? – Steven Clark Jul 17 '23 at 18:24
-
@StevenClark On your second comment: I am not sure that the limit integral representation you are using can be used for deltas supported in $z\in\Bbb C$. I had a quick look but it seems that Gel'fand and Shilov do use it. This is perhaps why it fails on a distribution which is supported in $z\in\Bbb C$. – Daniele Tampieri Jul 17 '23 at 18:29
-
Perhaps my Math StackExchange question on extending the Dirac delta function $\delta(x)$ for $x\in\mathbb{R}$ to $\delta(s)$ for $s\in \mathbb{C}$ is relevant. – Steven Clark Jul 17 '23 at 18:34
-
@StevenClark on your third comment: this is not correct. You car see this by using a $\delta$-converging sequence constructed by using a standard mollifier. I pointed out I avoided this approach since it is too much calculus intensive, however it can be done. Remember you are simply rotating a 1-D semi line. – Daniele Tampieri Jul 17 '23 at 18:41
-
@StevenClark on your fourth comment, I point out only this comment to the answer to your former question. – Daniele Tampieri Jul 17 '23 at 18:45
-
@StevenClark on your fifth comment: as you noticed, I did not used formula \eqref{1} in the evaluation of $\delta(x+i)$, according to my former comment. And there's nothing wrong with the second formula in your first comment as it is perfectly equivalent to mine, as $\delta(x+i)=\delta(ix-1)$. – Daniele Tampieri Jul 17 '23 at 20:05
-
1I think I understand your answer better now, so thanks for the feedback. – Steven Clark Jul 17 '23 at 20:06