1

I started with the following limit representation of the Dirac delta function:

$$\delta (x)=\underset{\epsilon\to 0}{\text{lim}}\left(\frac{\epsilon}{\pi\,\left(x^2+\epsilon^2\right)}\right),\quad x\in\mathbb{R}\tag{1}$$

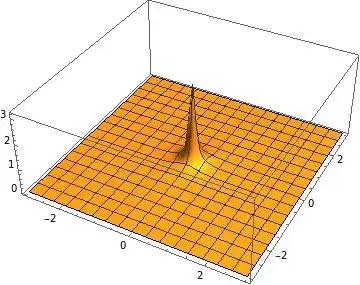
Figure (1) below illustrates $\delta (x)$ defined in formula (1) above evaluated at $\epsilon=0.1$

Illustration of formula (1)

Figure (1): Illustration of formula (1) for $\delta (x)$ evaluated at $\epsilon=0.1$.

I then attempted to extend the limit representation of $\delta(x)$ defined in formula (1) above to the complex plane as follows:

$$\delta(s)=\underset{\epsilon\to 0}{\text{lim}}\left(\frac{\epsilon}{\pi\,\left(s\,s^*+\epsilon^2\right)}\right),\quad s\in\mathbb{C}\tag{2}$$

Figure (2) below illustrates $\delta (s)$ defined in formula (2) above evaluated for $s\in\mathbb{C}$ using $\epsilon=0.1$.

Illustration of formula (2)

Figure (2): Illustration of formula (2) for $\delta (s)$ evaluated over the complex plane using $\epsilon=0.1$

Now consider the following integral of $\delta(s)$ defined in formula (2) above along the line $s=(a+i\,b)\,t$ where $a,b\in\mathbb{R}\land a^2+b^2=1$:

$$\int\limits_{-\infty}^\infty \delta((a+i\,b)\,t)\,\,dt=1\,,\quad a,b\in\mathbb{R}\land a^2+b^2=1\tag{3}$$

Integrating along the lines $s=t$ (where $a=1$ and $b=0$) and $s=i\,t$ (where $a=0$ and $b=1$) obviously meet the condition $a^2+b^2=1$ specified in formula (3) above. For the case $a\,b\ne 0$, if the line $s=(a+i\,b)\,t$ passes through the point $(c,i\,d)$ as well as the origin, then $a$ and $b$ can be calculated as

$$a=\frac{c}{d} \sqrt{\frac{1}{\frac{c^2}{d^2}+1}}\tag{4}$$

$$b=\sqrt{\frac{1}{\frac{c^2}{d^2}+1}}\tag{5}$$

or alternatively as

$$a=\sqrt{\frac{1}{\frac{d^2}{c^2}+1}}\tag{6}$$

$$b=\frac{d}{c} \sqrt{\frac{1}{\frac{d^2}{c^2}+1}}\tag{7}$$

Question: Can the Dirac delta function $\delta(x)$ for $x\in\mathbb{R}$ be extended to $\delta(s)$ for $s\in\mathbb{C}$ at least when integrated along the line $s=(a+i\,b)\,t$ where $a,b\in\mathbb{R}\land a^2+b^2=1$ as illustrated in formula (3) above?

Steven Clark
  • 7,363
  • I'm not terribly clear what you are asking or why. It look to me as if your required condition is met by the function you define in (3). – Blitzer Mar 07 '22 at 17:03
  • For any nonempty set $X$ and $x\in X$, you can consider $\delta_x$ as a measure (take the $\sigma$-algebra of all subsets of $X$ for example). That will extend $\delta_x$ to any space in a meaningful way. – Mittens Mar 07 '22 at 17:38
  • @Blitzer Yes, the integral defined in formula (3) evaluates to $1$ for the conditions specified in formula (3) using the limit representation defined in formula (2), and hence my question is specific to these conditions. I've read and been told the Dirac delta function $\delta(x)$ is only defined for $x\in\mathbb{R}$ but it seems to me it can perhaps be extended to the complexes assuming certain conditions which I've specified in my question. – Steven Clark Mar 07 '22 at 17:39

1 Answers1

3

The Dirac delta is not a function (in term of functions, your limit only converges to $0$ at every $x\neq 0$ and to $\infty$ when $x=0$ ...), the Dirac delta is a measure (or a distribution) defined by $$ \int_{\Bbb R} \varphi(x)\,\delta(\mathrm d x) = f(0) $$ for every continuous function $\varphi$. There is of course no problem to extend such a definition to complex functions by taking $\varphi$ to be complex valued and replacing the domain of integration by $\Bbb C$. This is the same as considering that $\Bbb C \simeq \Bbb R^2$. This complex Dirac delta would verify $$ \int_{\Bbb C} \delta(\mathrm d z) = 1. $$

Notice however that your approximation of the dirac Delta only works in dimension $1$ (it is not an integrable function in $\Bbb R^2$, so will not recover the above generalization of the dirac Delta that would be similar to a Dirac delta in $\Bbb R^2$. Your generalization rather converges as you write to a "radial" Dirac delta, so a function that has integral one along any line passing through $0$. It is usually rather written $\delta(|z|)$ with $|z| = \bar z \,z = a^2+b^2$ if $z=a+ib$. And this is because you just replaced $x$ by $|z|$ in your definition.

LL 3.14
  • 12,457
  • $\delta(x)=\left{\begin{array}{cc} \infty & x=0 \ 0 & x\neq 0\land x\in \mathbb{R} \ \end{array}\right.$ is not a sufficient characterization of the Dirac delta function. I've been told $g(x)\to\delta(x)$ if $\forall,f(x)\in C^\infty_c(\Bbb{R}), \int\limits_{-\infty}^\infty g(x)f(x)dx\to f(0)$. The function defined in formula (1) in my question is one example of a function $g(x)$ which meets this condition, and in fact Wolfram defines the Dirac delta function as formula (1) (see https://functions.wolfram.com/GeneralizedFunctions/DiracDelta/02/). – Steven Clark Mar 08 '22 at 15:55
  • There are other limit representations at https://functions.wolfram.com/GeneralizedFunctions/DiracDelta/09/. I've been told you can only prove things about $\delta(x)$ using these types of representations, so it seems to me an abstract definition is less useful than these types of representations. – Steven Clark Mar 08 '22 at 16:05
  • Also note that it is not sufficient to replace $x$ with $|z|=z,z^*$ where $z=(a+i,b),t$, $a$ and $b$ must also be selected such that $a^2+b^2=1$. – Steven Clark Mar 08 '22 at 17:03
  • When you say " Dirac delta in $\Bbb R^2$ ", do you mean as in $\int\limits_{-\infty}^\infty\int\limits_{-\infty}^\infty\delta(x,y),dx,dy=1$? If so then Wolfram seems to imply $\delta(x,y)=\frac{1}{\pi}\underset{\varepsilon\to 0}{\text{lim}}\frac{\varepsilon}{x^2+y^2+\varepsilon^2},\ x,y\in \mathbb{R}$ is a valid limit representation (see https://functions.wolfram.com/GeneralizedFunctions/DiracDelta2/02/), but I'm not sure this is correct. – Steven Clark Mar 08 '22 at 20:49
  • 1
    Please, Wolfram Alpha is not a good mathematical reference! The Dirac delta is defined by my first formula in the theory of distributions (see for example the book by Laurent Schwartz or any course on Distributions theory). Indeed, as I wrote, setting $\delta(0) = \infty$ does not mean anything so this is not a good definition. And indeed, your Formula (1) converges to a dirac Delta but in the sense of distributions and not in the sense of functions (pointwise convergence). – LL 3.14 Mar 09 '22 at 01:01
  • The abstract definition since it give a unique definition as a distribution, independent of the dimension or of a choice of approximation. Then as you write you can prove any approximation formula by proving something of the form $$ \int g_{\varepsilon} \varphi \to \varphi(0) $$ which is exactly the meaning of "convergence in the sense of distributions". This is the way to prove that your formula (1) indeed converges to a Dirac. Indeed, it might still be converging to a Dirac in higher dimensions, and now you know how to verify it ;) – LL 3.14 Mar 09 '22 at 01:05
  • Thanks for the clarification. I up-voted and accepted your answer. – Steven Clark Mar 09 '22 at 02:13