2

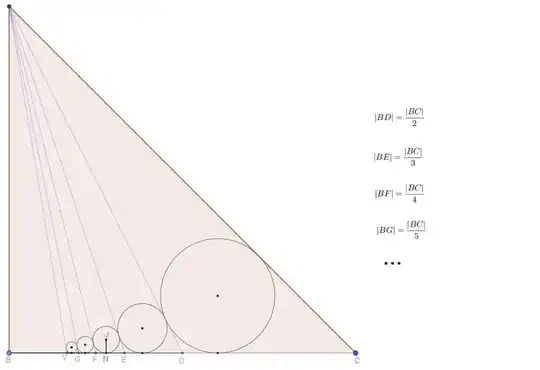
$ABC $ is an isosceles right triangle, whose small sides are $1$. I want to find a close form for the sum of the infinite radii of the small circumferences created by the cevians. The numerical value of this sum is $ 0.39709... $

Furthermore what kind of curve pass by the centers of the circles?

enter image description here

user967210
  • 711
  • 2
    This question reminds me of this recent one even if it is different... – Jean Marie Jun 09 '23 at 14:23
  • 1
    Here is a similar arrangement of circles, which has nice answers to the kinds of questions you are asking. If you draw tangent lines to the circles at the points where the circles touch each other, the tangent lines all meet at the same point $(2,2)$, so these tangent lines are cevians from a vertex of a triangle. The sum of the radii (excluding the biggest circle, which is outside the triangle) is $\frac{\pi^2}{6}-1$. The centres of the circles lie on $y=\frac14(x-2)^2$. – Dan Jun 10 '23 at 09:43
  • @Dan that's a nice discovery! But I guess that the answer is wrong because the circles radii are not decreasing like 1/n^2, the actual formula is given by the answer of Intelligenti pauca. By the way did you found a closed form for odd p? – user967210 Jun 10 '23 at 10:48
  • 1
    @user967210 I don't mean that the link in my previous comment answers your question here; I'm just saying that the link shows another arrangement of circles that has nice values. I didn't find a closed form for odd $p$. – Dan Jun 10 '23 at 10:53

1 Answers1

5

Using the formula for the inradius of a triangle it is easy to compute the $n$-th radius: $$ r_n={1\over 1+n\sqrt{n^2+2n+2}+(n+1)\sqrt{n^2+1}}. $$ The sum $\sum_{n=1}^\infty r_n$ is finite but Mathematica doesn't give a closed form for it, hence I doubt a nice formula can be found.

Intelligenti pauca
  • 50,470
  • 4
  • 42
  • 77