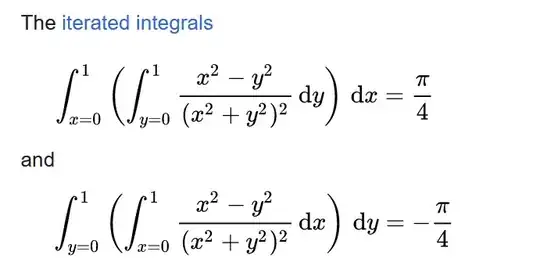The following question is about measure theory
I was looking at the calculations of the integrals withing this post Why the Fubini theorem fail??
I was wondering about this equality $\int\int\frac{\partial}{\partial y}(\frac{y}{x^2+y^2})=\int \frac{y}{x^2+y^2}\big|_{y = 0}^{y = 1}dx$. I know this is possible if $f(x,y)$ is continuous, but clearly, $f$ is not continuous at $0$. Does someone know what is the measure-theoric argument for the equality?
Remember that this is an iterated integration, which is a different thing than a double integration.
If we set up the integration in question properly (your cutting notational corners as you did may have been part of why you found this confusing), this is
$$\int_0^1\int_0^1 \frac{\partial}{\partial y}\frac y{x^2+y^2}\,dy\,dx$$
In particular, you can define the function $G(x) = \int_0^1 \frac{\partial}{\partial y}\frac y{x^2+y^2}\,dy$, and then the full integral is $$\int_0^1 G(x)\,dx$$
Now note that for $x > 0$, the integrand of the integral defining $G(x)$ is continuous for all $y\in[0,1]$. So $G(x) = \left.\frac y{x^2+y^2}\right|_0^1 = \frac1{1+x^2}$ for all $x > 0$ by the FTC.
But when $x = 0$, we get $$G(0) = \int_0^1 \frac{\partial}{\partial y}\frac y{y^2}\,dy = \int_0^1 \frac {-1}{y^2}\,dy = \left.\frac 1y\right|_0^1 = -\infty$$ So $G(0)$ is not defined, which makes the outer integral improper in Riemann theory, and isn't an issue in Lebesgue theory, since $\mu(\{0\}) = 0$. The lack of definition for $G$ at a lone point does not change the value of the outer integration. $\int_0^1\frac 1{1+x^2}\,dx = \frac\pi 4$.
