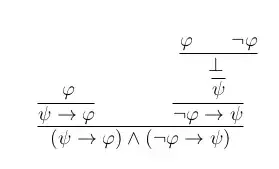Natural deduction problem: incomplete derivation

Question

Consider the following derivation of natural deduction:

Context: This is from a problem that asks for the student to "complete" the derivation, annotating its steps and any hypothesis cancellation.

My confusion: The right branch makes sense to me: from the contradictory hypotheses $\varphi, \neg\varphi$ we can derive any proposition $\psi$., from which we may conclude that $\neg \varphi \to \psi$.

The left branch, however, seems quite odd to me. How is $\psi \to \varphi$ derived from $\varphi$? Is this making use of the results on the right branch? If so, why are they separated?

It amounts to assuming psi, then phi and use Conditional Intro. — Mauro ALLEGRANZA, Apr 29 '23 at 13:32
But the assumption of psi is never explicitly stated. Only that of phi is declared. Is this standard? — lafinur, Apr 29 '23 at 16:12
Yes, of is allowed to use the rule like this even if the assumption doesn't actually occur. — Natalie Clarius, Apr 29 '23 at 23:12
And (I will insist, to make sure I understand), this is allowed because the "explicit way" (namely, assuming psi, then phi, then adding the implication) always involves canceling the assumption of psi? In other words, this is just an abbreviation of the implication rule, which involves cancelation ---it is not a different rule altogether. Is that right? — lafinur, Apr 30 '23 at 04:15

Natalie Clarius · Accepted Answer · 2023-04-30T22:58:20.693

1

It's just an application of $\implies I$. It is not required that the assumption $\psi$ actually occur in the subderivation.

Edit in response to your comment: It is a normal application of the implication introduction rule. The rule format with cancelling assumptions (in general, not just for implication introduction, but same for disjunction elimination) means that you are allowed to cancel such an assumption if there is one. You can also leave it open if for whatever reason you want to, or apply the rule without such an assumption at all. That's the general meaning of rules with discharging assumptions; you can cancel assumptions, but if you're fine even without it that's cool.

edited Apr 30 '23 at 22:58

answered Apr 29 '23 at 23:14

Natalie Clarius

10,530

Please see my response to your comment. Thanks for the answer btw – lafinur Apr 30 '23 at 04:16
See the edit to my post. – Natalie Clarius Apr 30 '23 at 22:59
You were very kind not only to answer my question but to take the extra time of clearing all my doubts. Thank you. – lafinur May 01 '23 at 22:42

Natural deduction problem: incomplete derivation

1 Answers1