2

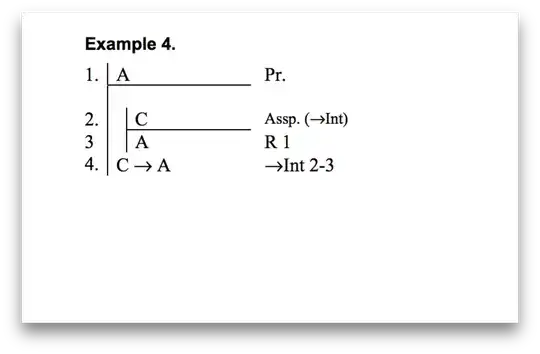
Apparently, according to the Conditional Introduction rule, this is valid: Prove $C \to A$ enter image description here

Source: http://kpaprzycka.wdfiles.com/local--files/logic/W12R Page 5

So before this, the way I viewed the CI rule, was that it allowed us to prove that if we assume the antecedent is true, we can prove the consequent can derived from the antecedent, by referring to the premises which lead to the consequent. If later we find that the antecedent is true, then we can conclude what we already done so before when we just assumed. So basically, sub derivations are inactive at first, but activated if the assumption of said sub derivation is confirmed.

In this example, it's basically stating that the mere assumption of some proposition is enough to state that it applies to some other already proven proposition. It's like you might as well skipped over the sub derivation and said, 'Given $A, C \to A$ because I want it to'.

Personally, I think this is a mistake, though if not, I can't see how you could justify that $C \to A$ given $A$ and assuming $C$ is true alone.

Mauro ALLEGRANZA
  • 94,169
user2901512
  • 2,080
  • That last "given that C is true alone" was a typo for "given that A is true alone"? Yes, this is perfectly valid. Why shouldn't it be? Suppose it's raining. Given that it's raining, the sentence "If it's Tuesday it's raining" is certainly true. – David C. Ullrich May 29 '16 at 15:46
  • "Personally, I think this is a mistake, though if not, I can't see how you could justify that $C\to A$ given that $C$ is true alone." You can't justify this because it's not true, and you've given some indication that you understand this. What you proved was $A\vdash C\to A$. – Git Gud May 29 '16 at 15:46
  • @DavidC.Ullrich but if you can infer anything, trivially so, the rule seems to lose value. I mean, what's the point? And it's not true that if it's tuesday then it's raining... – user2901512 May 29 '16 at 15:48
  • @GitGud Am not familiar with the sub derivation symbol by the way, but either way, given that A was the only premise, how could one prove anything else? – user2901512 May 29 '16 at 15:49
  • @user2901512 Can you accepted $A\vdash A\lor A$ and $A\vdash A\land A$? – Git Gud May 29 '16 at 15:52
  • Who said you could infer anything? You should really address questions, btw - is that last C a typo for A or not? – David C. Ullrich May 29 '16 at 15:52
  • @DavidC.Ullrich no not a typo, the 'proof' was assuming C, to conclude A, thus C -> A. We already knew A was true as it was stated as a proposition. – user2901512 May 29 '16 at 15:55
  • @GitGud, yes, I can accept that A v A and A^A is provable from itself. – user2901512 May 29 '16 at 15:57
  • Whatever - then the last sentence is simply wrong. We did not infer C->A assuming C alone. In fact we did not infer C->A assuming C! We inferred A assuming C. One cannot infer C->A assuming C alone - luckily that didn't happen. – David C. Ullrich May 29 '16 at 15:58
  • @user2901512 OK. Can you also accept that $A\vdash C\lor A$? – Git Gud May 29 '16 at 15:59
  • @DavidC.Ullrich Ah yes, my mistake, I meant to communicate given A and assuming C. – user2901512 May 29 '16 at 16:02
  • @GitGud I can't see how AvC is probable from A, no. – user2901512 May 29 '16 at 16:05
  • @user2901512 OK. I'm just trying to understand what's preventing you from getting this. Let me tell you something first. It holds that $A\vdash C\lor A$ simply because there's a rule in the system that says that from any statement $p$ you can infer $p\lor q$ whatever $q$ is. Is it what you want to understand why such a rule exists? – Git Gud May 29 '16 at 16:09
  • @user2901512 So if you looked out the window and saw it was raining, you wouldn't be sure whether the sentence "It's raining or it's Tuesday" was true or false? – David C. Ullrich May 29 '16 at 16:14
  • @GitGud Yes :) See if p is false then all you're left with q, yet there's no reason to believe that q implies p. Even if there was however, it wouldn't seem to matter, for if p is false, q can't imply p anyway, because we just said q is false. Yet, if p is true, p v q, whilst still true, is trivial, p can validate itself, due to the principle of identity. – user2901512 May 29 '16 at 16:14
  • @DavidC.Ullrich you said ''Given that it's raining, the sentence "If it's Tuesday it's raining" is certainly true''. – user2901512 May 29 '16 at 16:17
  • @user2901512 Yes, I said that. Several people have said several things. My last comment was regarding your problem with deriving $p\lor q$ from $p$... – David C. Ullrich May 29 '16 at 16:19
  • @user2901512 "Yet, if p is true, p v q, whilst still true, is trivial, p can validate itself, due to the principle of identity." OK, but when you look at $p\lor q$, you can't parse $p$ separately from the rest. You need to think like a computer, $p$ and $p\lor q$ are two different things and you need something to allow you to infer $p\lor q$ from $p$ other than your intuition or common sense. This is a formal system, formal systems need rules for every thing. In fact, you even need a rule to infer $p$ from $p$. – Git Gud May 29 '16 at 16:20
  • @DavidC.Ullrich oh ok, I get you. If you look outside, and see that it appears to be raining, it's (apparent) truth is certainly hard to deny. However, what if in fact it wasn't raining, and that the cause for the apparent rain was due to something else (say, a sprinkler upon the roof?). Why then, would that imply it was Tuesday? See it just doesn't follow. See I thought rules of inference was meant to have a tautological nature about them. – user2901512 May 29 '16 at 16:25
  • @DavidC.Ullrich Though upon further reflection I realized we first assumed A is true, not if it's not true. Thus yes, given A, A implies A v B. However, why is this itself of any value? – user2901512 May 29 '16 at 16:29
  • 1
    @user2901512 Your comment to Ullrich confirms something I've been suspecting. Please read this section of a Wikipedia article, you can also google conditional statement causality. But there are gaps in your knowledge other than this. – Git Gud May 29 '16 at 16:30
  • @user2901512 Your last comment is irrelevant to what I said. I didn't saying anything about looking outside and seeing that it appears to be raining. I said "If you looked out the window and saw that it was raining...". Questions about whether we can trust our senses may be fascinating, but they're irrelevant here. – David C. Ullrich May 29 '16 at 16:30
  • @GitGud, ok, I shall read what you reccomend and try to backtrack. – user2901512 May 29 '16 at 16:32

4 Answers4

2

In Natural Deduction, it is correct

given $A$, to derive $C \to A$.

See:

Consider as another case $A ⊃ (B ⊃ A)$.

Verbally, if we assume $A$, then $A$ follows under any other assumption $B$:

  1. $A$ --- hypothesis: goal $B ⊃ A$

  2. $B ⊃ A$ --- 1,$⊃$I

  3. $A ⊃ (B ⊃ A)$ --- 1–2,$⊃$I

This does not look particularly nice: we have closed an assumption $B$ that was not made. But if we say that an assumption was used $0$ times, the thing starts looking more reasonable.

This is nothing more that the "usual" axiom of Hilbert-style propositional calculus:

$\vdash A \to (B \to A)$

that of course is a tautology.

The idea is simply:

"if $A$ is true, then $B \to A$ is true also".

(This means that "$A$ is given" but in no way we have to assume that "$B$ is true also").

In classical logic, where we admit the equivalence of $p \to q$ and $\lnot p \lor q$, the above derivation is quite similar to:

  1. $A$ --- hypothesis

  2. $\lnot B \lor A$ --- 1,$\lor$I

  3. $A \to (\lnot B \lor A)$ --- 1–2,$\to$I

that looks "less weird".

Mauro ALLEGRANZA
  • 94,169
  • Wait... when you say 'used 0 times', do you mean that the conclusions drawn from said assumption cannot be validated and thus used until the assumption is validated? – user2901512 May 29 '16 at 16:21
1

It's not that $C\Rightarrow A$ just because you want it to be. The semantics of implication is defined as being true whenever the antecedent is false or the consequent is true. Since you know $A$ is true, by assumption, then it does not matter if $C$, or whatever other antecedent, is false or "unrelated" (as in "we know it is true that the Earth is round, therefore if unicorns have PhDs, then the Earth is round"). It's all about semantics.

Another way to see these facts is by this argument: a disjunction is defined as being true whenever one of its disjuncts is true. So if we know $A$ is true, it does not matter what we add to it by disjunction. The disjunction will still be true in virtue of $A$'s truth. Now, consider $\neg C\vee A$. We know that is true because of $A$'s truth. And since $\neg C\vee A$ is equivalent to $C\Rightarrow A$, one has justified the truth of the implication you were concerned with.

You may be wondering why one should accept something as my unicorns and Earth example if that is not intuitive at all. I suggest you research topics such as Strong/Strict Implication in non-classical logics. There are many cases when your intuition on the matter is correct, but it is not the case for classical logic.

Frank Hubeny
  • 1,527
Fernando Cano
  • 241
0

So, I can prove it without the rule of repetition as follows.

1 hypothesis   | A
2 1-1 -> Int    (A -> A)
3 assumption   | A
4 hypothesis   || C
5 2, 3 -> Elim || A
6 4-5 -> Int   | (C -> A)

Note that in the derivation of 2, I assumed the antecedent A as true, the consequent A got proved from the antecedent A, by referring to the premise A which lead to the consequent A. In this way, the repetition rule could get proved as a derivable rule of inference.

Doug Spoonwood
  • 11,211
0

4 years later...

Maybe a bit simpler, using another form of natural deduction...

enter image description here

Dan Christensen
  • 14,529