-1

$$\color{white}{\require{cancel}{.}}$$So I was again looking through the homepage of Youtube to see if there were any math equations that I thought that I might be able to solve when I came across this video by Cipher. The question in the video in question was $$\text{Prove that for any positive integer }n\text{, }2903^n-803^n-464^n+261^n\text{ is divisible by }1897$$which I thought that I might be able to do.

Here is my attempt at proving the aforementioned statement

Restrictions that I am going to place down right away:

  1. We know that we are going to have to make the assumption that $n$ cannot be a number that is in the set of all whole numbers$$n\in\mathbb{W}$$since not all real numbers are divisible.
  2. For the duration of this question, I am going to assume that $n\neq0$ since it would probably be easier to prove if we used $0$ as an example (since $\frac{0}{1897}\text{ is just }0$), so$$n\in\mathbb{W}\text{ where }n\gt0$$

Set up a table $x, y, z$, where $x$ is the number that we are going to plug in for $n$, $y$ is the output, and $z$ is the number that we get when we divide the output by $1897$.

$x$ $y$ $z$
$0$ $0$ $0$
$1$ $1897$ $1$
$2$ $7635425$ $4025$
$3$ $23864868937$ $12580321$

See? Everything's going well at this point! Now, what happens when we plug in $x=4$?$$2903^4-803^4-464^4+261^4=70563731909825$$That doesn't look to bad, besides it being a bit of a large number! Now lets see what happens when we divide it by $1897$!$$\frac{70563731909825}{1897}\approx3.719753922\cdot10^{10}$$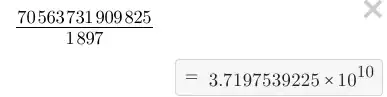enter image description here$$\color{white}{.}$$Also doesn't look too bad, however, just to make sure, I'll multiply the denominator by $10^{10}$ to see if it actually is $3.7197539225×10^{10}$ exactly.$$\frac{70563731909825}{1987\cdot10^{10}}\approx3.55126984951$$$$\therefore\text{ for any }n\text{ where }n\in\mathbb{W}\text{ and }n\gt0$$$$2903^n-803^n-464^n+261^n\text{ is divisible by 1897 for }0\lt n\leq3$$

My question

Did I do something wrong, and if I did, what could I do to prove/disprove it more easily? I am not that great at proof by induction (i.e. I don't really understand it), so it might not be able to help me a whole lot.

CrSb0001
  • 2,532
  • Note that $1897=7\cdot 271$. Use little Fermat, i.e., $a^7\equiv a \bmod 7$, to show that it is divisibly by $7$, and similarly also by $271$. – Dietrich Burde Apr 26 '23 at 14:41
  • For $n=4$, the expression is indeed divisible by $1897$: https://www.wolframalpha.com/input?i=%282903%5E4%E2%88%92803%5E4%E2%88%92464%5E4%2B261%5E4%29%2F1897 – Levent Apr 26 '23 at 14:44
  • @Levent Oh okay I must've messed up with my math somewhere then. – CrSb0001 Apr 26 '23 at 14:45
  • 1
    For a solution-verification question to be on topic you must specify precisely which step in the proof you question, and why so. This site is not meant to be used as a proof checking machine. – Bill Dubuque Apr 26 '23 at 16:24
  • This answer in the linked dupe explains the innate symmetry that enables great simplifications in these types of problems. – Bill Dubuque Apr 26 '23 at 16:28
  • As mentioned, your arithmetic is incorrect for the $n=4$ case. Nor can you prove it for all $n$ brute force checking every case. It's best for site health to delete questions based on arithmetic errors. – Bill Dubuque Apr 26 '23 at 18:48

1 Answers1

1

Note that $1897 = 7 \times 271$ and $2903^{n} - 803^{n} - 464^{n} + 261^{n} \equiv_{7} 5^{n} - 5^{n} - 2^{n} + 2^{n} \equiv_{7} 0$ and $2903^{n} - 803^{n} - 464^{n} + 261^{n} \equiv_{271} 193^{n} - 261^{n} - 193^{n} + 261^{n} \equiv_{271} 0$.

conan
  • 1,234