8

Update: Posted in MO since it is unanswered in MSE

Let $0 \le x,y \le 1$ and $a$ be a real. Consider the function

$$ f(x,y,a) = xy^{y^a/x^a} + yx^{x^a/y^a} - x^a - y^a \tag 1 $$

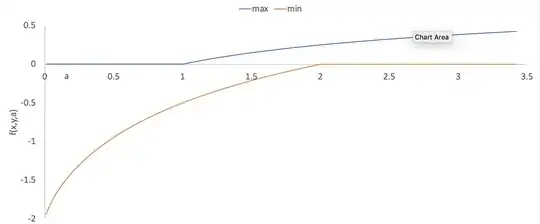
For a fixed $a$, the graph of the maximum and the minimum value of $f(x,y,a)$ shown below.

enter image description here

The graph shows that for $a \ge 1$, there is a constant $C_a$ depending only in $a$ such that $xy^{y^a/x^a} + yx^{x^a/y^a} - y^a - x^a \le C_a$ and similarly for $a \le 2$, there is a constant $c_a$ such that $c_a \le xy^{y^a/x^a} + yx^{x^a/y^a} - y^a - x^a$. Also, $0\ <a < 2$ is the only interval in which $f(x,y,a)$ has non-zero maxima and minima for every $a$.

Some experimentally observed examples of inequalities belonging to this family are

$$ -\frac{1}{2} \le xy^{y/x} + yx^{x/y} - x - y < 0 \tag 2 $$

$$ 0 \le xy^{y^2/x^2} + yx^{x^2/y^2} - x^2 - y^2 \le \frac{1}{4} \tag 3 $$

$$ 0 \le xy^{y^4/x^4} + yx^{x^4/y^4} - x^4 - y^4 \le \frac{1}{2} \tag 4 $$

Question 1: Can we prove that for every real $a$, there exists $c_a$ and $C_a$ such that

$$ c_a \le xy^{y^a/x^a} + yx^{x^a/y^a} - x^a - y^a \le C_a $$

Question 2: Can we express $c_a$ and $C_a$ in terms of $a$?

Nilotpal Sinha
  • 19,424
  • Do you want to prove the inequality in the title i.e. $a = 2$, or answer your Question 1, 2? – River Li Apr 21 '23 at 13:32
  • @RiverLi I have updated the title to make it consistent – Nilotpal Sinha Apr 21 '23 at 13:36
  • I think the more fitting title would be like "for some constants $c_a,C_a$" instead of "for all $a$", because the latter is implicitly implied by the former. – bluebril Apr 21 '23 at 13:39
  • Is $a$ positive or any sign? – Aleksandr Kalinin Apr 21 '23 at 21:41
  • note that since $y^a/x^a \ge 0$ we have $0 \le y^{y^a/x^a} \le 1$ for $0 \le y \le 1$ so the expression is at most $x+y-x^a-y^a \le 2$ for example and at least $-x^a-y^a$ which is bounded inferior for $a \ge 0$ by $-2$; of course if $a<0$ the expression is inferior unbounded as fixing $y$ and letting $x \to 0$ say makes it go to minus infinity; the better question is of tighter bounds eg for which $a$ the expression is non negative etc – Conrad Apr 21 '23 at 21:49
  • @Conrad If $a$ can be negative it does not work, that is why I asked. – Aleksandr Kalinin Apr 21 '23 at 22:14
  • @Aleksandr yes if $a<0$ the expression is unbounded inferior as noted – Conrad Apr 21 '23 at 22:15

0 Answers0