some values of sine function

Question

how to show that

$$\sin \frac{\pi}{10} = \frac{\sqrt5 - 1}{4}$$ $$\sin \frac{\pi}{60} = \dfrac{\sqrt{30} + \sqrt{10} + \sqrt{20 + 4 \sqrt5} - \sqrt6 - \sqrt2 - \sqrt{60 + 12 \sqrt5}}{16}\,\!$$ $$\sin \frac{7\pi}{15} =\frac{\sqrt{10 - 2\sqrt5} + \sqrt{15} + \sqrt3}{8}$$

I know that $\sin \frac{\pi}{4}=\cos \frac{\pi}{4}=\frac{\sqrt 2}{2}$ because of 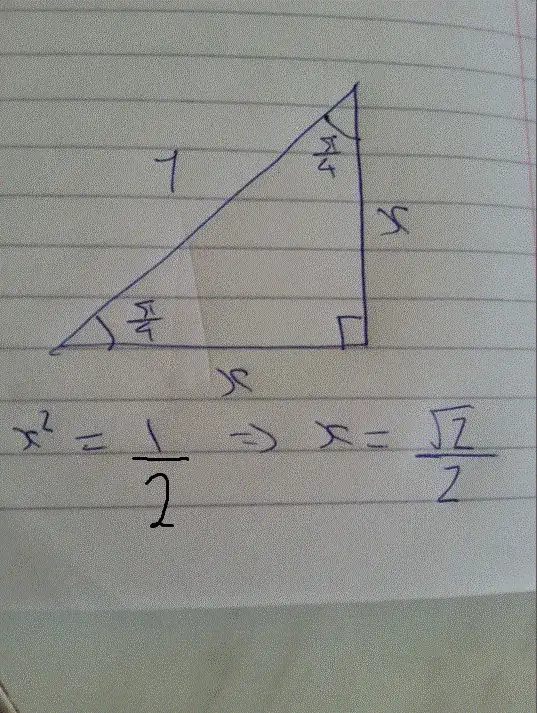enter image description here

but what about the other values ??? how to find them using analytic way or geometric way ?

See this for $\sin (\pi/10)$. – David Mitra Aug 14 '13 at 11:25 — David Mitra, Aug 14 '13 at 11:25
See this for $\sin (\pi/60)$ (and other values). – David Mitra Aug 14 '13 at 11:31 — David Mitra, Aug 14 '13 at 11:31

score 2 · Accepted Answer · answered Aug 14 '13 at 11:27

2

I googled "Sine of 36" and I found this webpage. It supplies explanations and links to pages with other explanations for a whole host of angles.

answered Aug 14 '13 at 11:27

Fly by Night

32,272

some values of sine function

1 Answers1