The strange case about the outer face...

Question

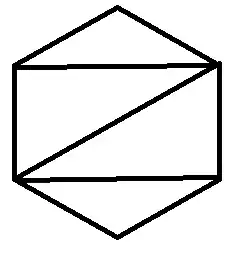
Let $f_k$ denote the face degree of a cubic planar graph, then from Euler's Formula it follows that: $$ \sum_{k=1}^F f_k = 6F-12 \tag{1} $$ Now I tried to construct some graphs from that, so let $F=4$ and from $(1)$ we get: $6\cdot4-12=12=\sum f_k$ and so it follows that $f_k=3, \forall k$. Fine. Let's continue with $F=5$: One partition might look like $ 6\cdot 5 -12=18=3+3+3+3+6$. At this point I decided to draw the graphs:

$\hskip1.4in$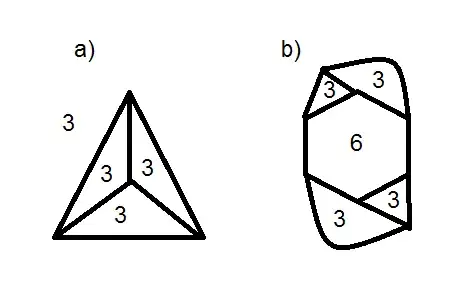 enter image description here

The strange thing is that I had to include the outer face in a) but not in b). My reasoning seems to be broken. What did I miss?

Here's my attempt to proof a slightly more general form of $(1)$... — draks ..., Aug 13 '13 at 19:40
You drew a different graph with $F=6$ instead of the graph you wanted. Try triangulating a hexagon instead. — , Aug 13 '13 at 19:56

coffeemath · Accepted Answer · 2013-08-14T00:03:01.363

The graph (b) you have here has 6 faces, including the "outer" face, so the calculation should be $6\cdot 6-12=24.$ And since the outer face has also 6 edges, the other sum is $6+6+3+3+3+3=24.$

ADDED: I think what happens here is that, by not using the outer face, the number $F$ in $6F-12$ goes down by $1$, causing that expression to go down by $6$, and it just so happens in your example that your outer face has also $6$ edges, so that by not counting those, the "edge sum" also goes down by 6. So the two equalities both holding on inclusion or exclusion of the outer face can only happen provided the outer face happens to have six edges.

score 0 · Answer 2 · edited Apr 13 '17 at 12:20

0

Thanks to Rahul:

$\hskip2.2in$ enter image description here

edited Apr 13 '17 at 12:20

Community

1

answered Aug 18 '13 at 19:46

draks ...

18,449

The strange case about the outer face...

2 Answers2