Henning once told me that,
[i]t follows from the Euler characteristic of the plane that the average face degree of a 3-regular planar graph with $F$ faces is $6-12/F$, which means that every 3-regular planar graph has at least one face with degree $5$ or lower.
I tried to understand and extend this and got the following:
Given a $k$-regular graph. Summing over the face degrees $f_n$ gives twice the number of edges $E$ and this is $k$ times the number of vertices $V$: $$ \sum f_n = 2E =kV \tag{1} $$ Further we have Euler's formula saying $$ V+F = E +\chi, $$ where $\chi$ is Euler's characteristic of the surface where the graph lives on. Again we insert $E=\frac k2V$ and get: $$ F=\left( \frac k2 -1 \right)V+\chi\\ V=\frac{F-\chi}{\frac k2 -1}. \tag{2} $$ Dividing $(1)$ by $F$ and inserting $(2)$ gives: $$ \frac{\sum f_n}{F}= \frac{k(F-\chi)}{(\frac k2 -1)F}=\frac {2k}{k -2} \left( 1-\frac{\chi}{F}\right) \tag{3} $$
or
$$ \sum f_n=\frac {2k}{k -2} \big( F-\chi\big). \tag{3$^\ast$} $$
Plug in $k=3$ and $\chi=2$ (the characteristic of the plane), we get back Henning's formula, but when e.g. $\chi=-2$, so the surface we draw could be a double torus, we get the average degree to be:
$$ 6 \left( 1+\frac{2}{F}\right) $$
How to find cubic graphs where the $\min(f_k)>6$ on surfaces with $\chi<0$?
EDIT The graph should not be a snark.
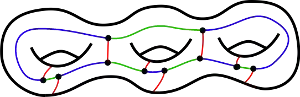
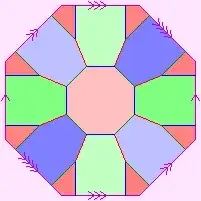
Embedding scheme on page 5 of http://www.math.caltech.edu/~2012-13/2term/ma006b/12Ma6bChp35.pdf – jp26 Aug 04 '13 at 20:30