Yes, your suspicion is right; the limit exists and it converges to $0.5221$.
Let $p_n$ be the $n$-th prime. We have $E_{p_n} = \frac{p_n}{(p_n-1)^2} = \frac{1}{p_n} + \frac{2}{p_n^2} + \frac{3}{p_n^3} + \cdots = \frac{1}{p_n} + f_{p_n}$
where $f_{p_n} = \frac{2}{p_n^2} + \frac{3}{p_n^3} + \cdots$. We have
$$
2^{E_2} 3^{E_3} ... q^{E_{p_n}} = (2^{\frac{1}{2}} 3^{\frac{1}{3}} ... p_n^{\frac{1}{p_{n}}}) . (2^{f_2} 3^{f_3} ... p_n^{f_{p_n}}) \tag 1
$$
Let us look at the two parts $2^{\frac{1}{2}} 3^{\frac{1}{3}} ... p_n^{\frac{1}{p_n}}$ and $2^{f_2} 3^{f_3} ... p_n^{f_{p_n}}$ separately.
For the first part, Mertens first theorem states that $ \sum_{ p \le p_n } \frac{\log p}{p} = \log p_n + B_3 + o(1)$ where $B_3 \approx 1.332582$ is the Merten's constant. Hence
$$
2^{1/2} 3^{1/3} ... p_n^{1/p_n} \approx p_n e^{-B_3} \tag 2
$$
For the second part, we have
$$
2^{f_2} 3^{f_3} 5^{f_5}... p_n^{f_{p_n}} = \prod_{i = 1}^n p_i^{\sum_{k = 2}^{\infty} \frac{k}{p_i^k}} = \prod_{i = 1}^n p_i^{\frac{2p_i - 1}{p_i(p_i-1)^2}} \tag 3
$$
For the closed form of the sum on the above exponent, refer to this link. Hence,
$$
\lim_{p \to \infty}r(p) = \lim_{n \to \infty}{ p_{n+1} \over 2^{1/2} 3^{1/3} ... p_n^{1/p_n}} \cdot { 1 \over 2^{f_2} 3^{f_3} ... p_n^{f_{p_n}}} = \lim_{n \to \infty} \frac{e^{B_3} p_{n+1}}{p_n} \cdot \prod_{i = 1}^n p_i^{-\frac{2p_i - 1}{p_i(p_i-1)^2}} \tag 4
$$
Since $\frac{p_{n+1}}{p_n} \to 1$ as $n \to \infty$, $(4)$ reduces to
$$ \lim_{p \to \infty}r(p) = e^{B_3} \prod_{p} p^{-\frac{2p - 1}{p(p-1)^2}} \approx 0.522174 $$
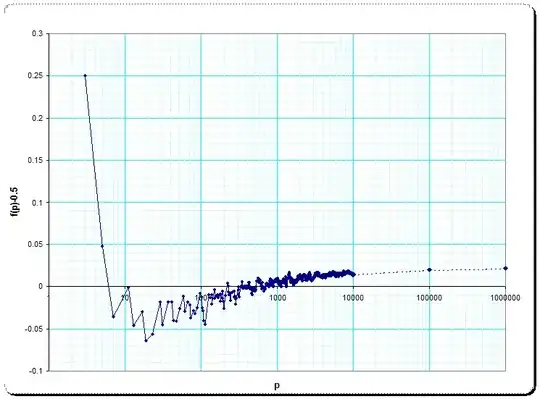 Another graphic with x-scale doubly logarithmic:
Another graphic with x-scale doubly logarithmic:
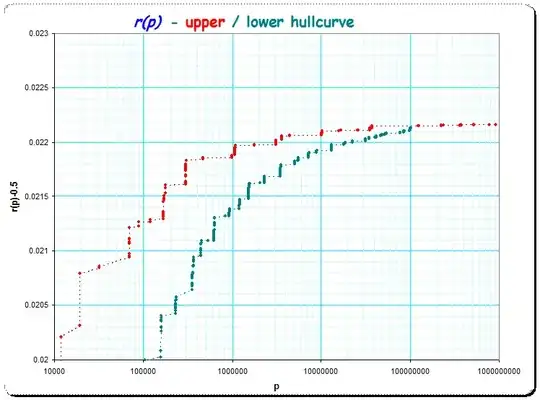
 A graphic showing even more values (up to $p \lt 10^8$) but the upper and lower hullcurves giving some suggestion for convergence:
A graphic showing even more values (up to $p \lt 10^8$) but the upper and lower hullcurves giving some suggestion for convergence: