history:
- 1st version
- update : frequency tables (on $N=800\,000$)
- update2: reliability of estimate of $\hat q_\text{go}$ for $N \to \infty$
- update3: estimates for $\hat q_{\text{go},p}$ for general $p$ instead of $7$
A heuristic frequencies list using only $a_{r}$ from the first $800\,000$ numbers $a_{r} \in \mathbb N^+ \mathbb{/2/3/5}$ beginning with $[1, 7, 11, 13, 17, 19, 23, 29, 31, 37]$.
Using $p=7$ I compute $w_{r} = p \cdot a_{r}+1$ then $b_{r}= \{w_{r}\}_{2,3,5} $ and $q_{r}=w_{r}/b_{r}$ . Here the notation $ \{n\}_s$ means complete extraction of all primefactors given in the list $s$ from natural number $n$.
In the following the absolute and the relative frequencies of $q_{r}$ (partially reordered hoping this gives a better sense for the patterns):
q_r frq(q_r) relfrq(q_r) % N=800 000
-------------------------------------------------
2 150000 18.7500000000
4 75000 9.37500000000
8 37500 4.68750000000
16 18750 2.34375000000
32 9375 1.17187500000
64 4687 0.585875000000
128 2343 0.292875000000
...
6 100000 12.5000000000
12 50001 6.25012500000
24 25000 3.12500000000
48 12500 1.56250000000
96 6249 0.781125000000
...
18 33332 4.16650000000
36 16666 2.08325000000
72 8334 1.04175000000
144 4166 0.520750000000
...
10 40000 5.00000000000
20 20000 2.50000000000
40 10000 1.25000000000
80 5000 0.625000000000
...
50 8000 1.00000000000
100 4000 0.500000000000
200 2000 0.250000000000
400 1000 0.125000000000
...
54 11112 1.38900000000
108 5556 0.694500000000
...
30 26667 3.33337500000
60 13333 1.66662500000
120 6667 0.833375000000
...
90 8889 1.11112500000
150 5334 0.666750000000
160 2500 0.312500000000
162 3704 0.463000000000
180 4445 0.555625000000
192 3125 0.390625000000
...
216 2777 0.347125000000
...
...
In the "relfrq%" columns in relative fractional expression:
q_r frq(q_r) relfrq(q_r) N=800 000
-------------------------------------------------
2 150000 3/16
4 75000 3/32
8 37500 3/64
16 18750 3/128
...
6 100000 1/8
12 50001 1/16
24 25000 1/32
48 12500 1/64
96 6249 1/128
...
10 40000 1/20
20 20000 1/40
40 10000 1/80
80 5000 1/160
...
18 33332 1/24
36 16666 1/48
72 8334 1/96
144 4166 1/192
...
30 26667 1/30
60 13333 1/60
120 6667 1/120
...
50 8000 1/100
100 4000 1/200
...
54 11112 1/72
108 5556 1/144
...
90 8889 1/90
150 5334 1/150
180 4445 1/180
...
Update
Here are my frequencies-tables. Each table is understood as increasing exponents at $3$ along rows(downwards) and increasing exponents at $5$ along columns (rightwards), each beginning with exponents $0$.
The separate tables are according to increasing exponents of $2$. The first table is empty because they are no cases, where the exponents at $2$ are zero. The last row,column,table are accumulated frequencies for exponents larger or equal than $6$:
0 0 0 0 0 0 0 |
0 0 0 0 0 0 0 |
0 0 0 0 0 0 0 |
0 0 0 0 0 0 0 | for exponent 2^0
0 0 0 0 0 0 0 |
0 0 0 0 0 0 0 |
0 0 0 0 0 0 0 |
- - - - - - - +
150000 40000 8000 1600 320 64 16 | Example 320 cases with 2^1*3^0*5^4
100000 26667 5334 1067 213 42 11 | 213 cases with 2^1*3^1*5^4
33332 8889 1777 356 71 15 3 |
11112 2962 593 118 24 5 1 | for exponent 2^1
3704 988 197 39 8 1 1 |
1234 330 66 13 2 1 0 |
618 164 33 7 2 0 0 |
- - - - - - - +
75000 20000 4000 800 160 32 8 |
50001 13333 2666 533 107 22 5 |
16666 4445 889 178 35 7 2 |
5556 1482 296 59 12 2 1 | for exponent 2^2
1851 494 100 20 3 1 0 |
617 164 33 7 2 0 0 |
309 82 16 3 1 0 0 |
- - - - - - - +
37500 10000 2000 400 80 16 4 |
25000 6667 1333 266 53 11 3 |
8334 2222 445 89 18 3 1 |
2777 740 149 30 6 1 0 | for exponent 2^3
925 247 49 10 3 0 0 |
309 82 16 3 0 1 0 |
155 42 8 2 0 0 0 |
- - - - - - - +
18750 5000 1000 200 40 8 2 |
12500 3333 667 134 27 5 1 |
4166 1111 222 45 9 2 0 |
1390 370 74 14 3 1 0 | for exponent 2^4
463 124 24 4 1 0 1 |
155 42 8 2 0 0 0 |
76 20 5 1 0 0 0 |
- - - - - - - +
9375 2500 500 100 20 4 1 |
6249 1666 333 67 14 3 0 |
2085 556 111 21 4 1 1 |
694 186 37 8 1 0 0 | for exponent 2^5
231 62 13 3 0 0 0 |
77 20 5 1 0 0 0 |
39 10 1 0 1 0 0 |
- - - - - - - +
9375 2500 500 100 20 4 1 |
6250 1668 333 67 12 3 1 |
2083 554 112 22 6 0 0 | accumulated
694 186 36 8 1 1 0 | for exponents 2^(6..oo)
233 60 13 2 1 0 0 |
76 22 3 1 0 0 0 |
39 10 3 0 0 0 0 |
- - - - - - - +
The counting the occurences of primefactors 2,3,5 (respecting their multiplicities as well) I get the average quotient as $\hat q_\text{go} = 2^2 \cdot 3^{3/4} \cdot 5^{5/16} \approx 15.077$
This is little but systematically different from yours where you have $\hat q_\text{mick} = 2^2 \cdot 3^{2/4} \cdot 5^{4/16} \approx 10.36$.
I'm not completely sure of my result because of finitety of the frequencies tables (and maybe overlooking something). The extrapolation of the heuristical tables using the rules of geometric series (to fill up the missing frequencies for higher exponents) give a change only less than $0.01 \text{%} $ and so I'm now somehow confident of my estimate.
Update 2 Improving reliability of estimate for $\hat q_\text{go}$ .
To see, how increase of $N$ (number of used initial numbers $a_r$) increases accuracy of estimate of $\hat q_\text{go}$ I've now made a small but efficient program which shows, that my given estimates for the quotient $q$ are very likely correct.
Pari/GP-program:
p=7;
N=30000000;
{s2=s3=s5=0;n7=0;
forstep(a1=1,N ,[6,4,2,4,2,4,6,2],n7++; \\ a1<--[1,7,11,13,17,...]
w1=p*a1+1;
e2=valuation(w1,2);s2+=e2;
e3=valuation(w1,3);s3+=e3;
e5=valuation(w1,5);s5+=e5;
);
print(n7," ",[s2,s3,s5]/n7*1.0);}
This gives for increasing $N$:
n7 expon at 2 expon at 3 expon at 5
-------------------------------------------------------------
8000 [2.00025000000, 0.750625000000, 0.312500000000]
80000 [2.00007500000, 0.750037500000, 0.312525000000]
800000 [2.00000500000, 0.750001250000, 0.312501250000]
8000000 [2.00000087500, 0.750000000000, 0.312500000000]
This is obvious convergence to $\hat q_{go}=2^2 \cdot 3^{3/4} \cdot 5^{5/16}$
Update 3: Generalizing to $px+1$ with $p<>7$ .
If we insert any $p>2$ into the basic formula $px+1$ and define the divisor by the sequence of all smaller primes then we find heuristically
$$ \begin{array} {}
\hat q_{\text{go},3} & = 2^ 2 \\
\hat q_{\text{go},5} & = 2^ 2 \cdot 3^{3/4} \\
\hat q_{\text{go},7} & = 2^ 2 \cdot 3^{3/4} \cdot 5^{5/16}\\
\hat q_{\text{go},11} & = 2^ 2 \cdot 3^{3/4} \cdot 5^{5/16}\cdot 7^{7/36}\\
\end{array} \tag {3.1}
$$
from where I guess, we can continue this in the obvious way.
This gives as decreasion-ratio per step for $p=3$ : $ r_p = p/ \hat q_{\text{go},3} = 0.75 $, for $p=5$ : $ r_p = p/ \hat q_{\text{go},5} = 0.548364172064 $ and so on, which for higher $p$ seems to converge to some value near $0.5221...$ (but convergence is extremely slow and possibly no convergence occurs at all)
Here are some few first decrease-ratios:
p r_p
--------------------------
3 0.750000000000
5 0.548364172064
7 0.464268246566
11 0.499734125829
13 0.453666258060
17 0.470627952355
19 0.435785623530
23 0.443872763259
29 0.482190280028
31 0.455080623128
37 0.482568810773
41 0.482358783004
43 0.459967559885
47 0.458710305317
53 0.474871755038
59 0.489052691745
61 0.470733529185
...
9941 0.514336091023
9949 0.514273517069
9967 0.514727391276
9973 0.514561607904
...
99961 0.520162302125
99971 0.520154427675
99989 0.520188173244
99991 0.520138684311
...
999931 0.521839942933
999953 0.521844214134
999959 0.521840135480
999961 0.521833969462
999979 0.521836153082
999983 0.521831030904
...
9999929 0.522079299112
9999931 0.522078562031
9999937 0.522078033784
9999943 0.522077505537
9999971 0.522078125867
9999973 0.522077388790
9999991 0.522077487040
...
99999773 0.522130942161
99999787 0.522130919079
99999821 0.522131000424
99999827 0.522130935571
99999839 0.522130902047
99999847 0.522130847637
99999931 0.522131190048
99999941 0.522131146080
99999959 0.522131143884
99999971 0.522131110360
99999989 0.522131108163
...
905041847 0.522168528916
905055527 0.522168532733
905055559 0.522168539297
905055623 0.522168540525
905055691 0.522168544062
...
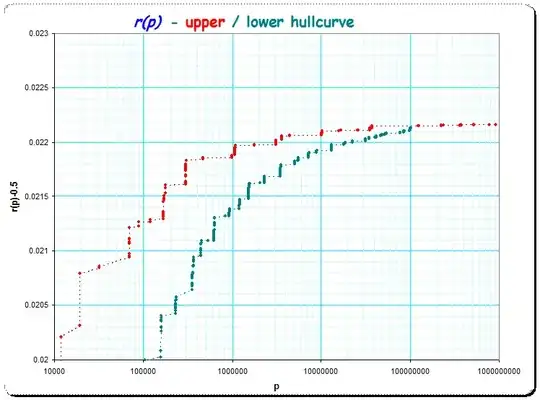
I took this up to $N =100\,000\,000$ , $p_N=2\,038\,074\,743 $ giving the following picture for $r_p-0.5$ depending on $p$ (for the higher primes I only show the values near $p \approx 10^k$ and linear interpolation by Excel (dotted lines)):
 And the upper & lower hullcurve (upper hullcurve up to $p_N=
And the upper & lower hullcurve (upper hullcurve up to $p_N=


https://math.stackexchange.com/a/4658056 (an answer of mine for the 2nd Q)
https://math.meta.stackexchange.com/a/4726 (beginning of working out formulae for the general case) and I have a vague idea I have seen the (fully generalized) thing once on mathoverflow, but a short search didn't find anything...
– Gottfried Helms Mar 25 '23 at 15:03