Is there a name for the hyperbola and ellipse with same minor and major axes?

Question

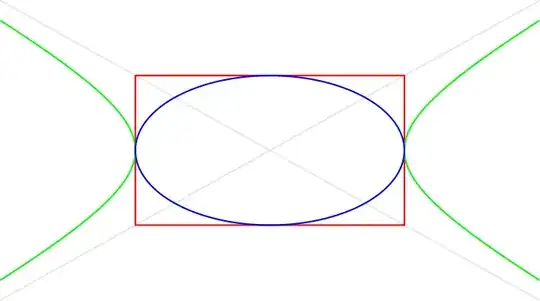
The equation for an ellipse is $x^2 / a^2 + y^2 / b^2 = 1$ and that of the hyperbola is $x^2 / a^2 - y^2 / b^2 = 1$.

I consider the case when an ellipse and hyperbola defined as above share the same $a$ and $b$ values. That is, when they have the same length of (semi) major and minor axes and same center. (They also seem to have the same curvature but of opposite sign at their [common] vertices.)

They would be geometrically related in as the bounding rectangle of the ellipse would have its corners on the asymptotes of the hyperbola:

My question is whether there is any name for or any specific words or to express this relation between of ellipse and hyperbola. I mean something like “in-ellipse of the hyperbola” or “ex-hyperbola of the ellipse”…

Answer 1

Loosely speaking, they may be called conjugates.

• Ellipse

$$\frac{x^2}{\alpha^2}+\frac{y^2}{\beta^2}=1$$

• Conjugate hyperbolae

$$\frac{x^2}{\alpha^2}-\frac{y^2}{\beta^2}=1$$

$$\frac{y^2}{\beta^2}-\frac{x^2}{\alpha^2}=1$$

• The area of parallelogram with conjugate diameters as diagonals is constant:

$$S=2\alpha \beta$$

• The conjugate diameter of a hyperbola meet its conjugate (hyperbola) only.

• The axis cuts the vertices of a hyperbola is called transverse axis while the other is called conjugate axis. They flip the roles for conjugate hyperbola.

• The foci of two hyperbolae lies on the director circle of the ellipse.

• The foci of the ellipse lies on the director circle of one hyperbola.

• Compare conjugate conics, which are the focal conics, of confocal quadrics here.