Let $x>0$, $\theta \le 1$, $\mu_0 \in {\mathbb R}$ and $\nu:= -{\bar \mu_0}/(1-\theta)$ and ${\bar \mu_0} := \mu_0 - 1/2 $. Now, consider a non-linear diffusion model $d X_t = \mu_0 X_t^{2 \theta-1} dt + X_t^{\theta} d B_t $ subject to $X_0 = x$ where $B_t$ is the Brownian motion.
By using my answer to this question and the fact that the probability density of a running supremum is equal to the anti-derivative with respect to time from the density of the first hitting time, i.e. $P\left( \text{sup}_{0 \le t \le T} X_t > b \right) = \int\limits_0^T \rho_{\tau_b}(t) dt $ where $\rho_{\tau_b}(t) := P \left( t \le \tau_b \le t+dt \right)/dt$ and $\tau_b := \text{inf}\left( t \ge 0 | X_t > b \right) $ it can be shown that the following identity holds true:
\begin{eqnarray} P\left( \text{sup}_{0 \le t \le T} X_t > b \right) = 2 \imath \sum\limits_{\xi=1}^\infty \left[1 - e^{-\frac{T}{2} b^{2 \theta-2} (1-\theta)^2 [ \zeta_\xi^{(-\nu)}]^2} \right] \cdot \left( \frac{x}{b} \right)^{\frac{1}{2} - \mu_0} \cdot \frac{I_{-\nu}\left[(\frac{x}{b})^{1-\theta} \imath \zeta_\xi^{(-\nu)} \right]}{ \zeta_\xi^{(-\nu)} \cdot I^{'}_{-\nu} \left[ \imath \zeta_\xi^{(-\nu)}\right]} \tag{1} \end{eqnarray}
where $b > x$. Here $ \left( \zeta_\xi^{(-\nu)} \right)_{\xi=1}^\infty $ are zeros of the Bessel function $J_{-\nu}\left( \cdot \right) $.
Now, I am concerned with calculating the limit $\theta\rightarrow 1_-$ of the quantity in $(1)$. I will compute this in two different ways with the first way expressing the quantity in question through an inverse Laplace transform and the second way relying entirely on properties of the Bessel functions.
First way:
\begin{eqnarray} &&\lim\limits_{\theta \rightarrow 1_-} P\left( \text{sup}_{0 \le t \le T} X_t > b \right) = \\ &&\lim\limits_{\theta \rightarrow 1_-} \frac{1}{2 \pi \imath} \int\limits_{\imath {\mathbb R}- \cdots} \frac{-1 + e^{\alpha T} }{\alpha} \cdot \left( \frac{x}{b} \right)^{\frac{1}{2} - \mu_0} \cdot \underline{ \frac{I_{-\nu} \left[ \frac{x^{1-\theta}}{1-\theta} \sqrt{2 \alpha}\right]}{I_{-\nu} \left[ \frac{b^{1-\theta}}{1-\theta} \sqrt{2 \alpha}\right]}} d \alpha = \\ && \frac{1}{2 \pi \imath} \int\limits_{\imath {\mathbb R}- \cdots} \frac{-1 + e^{\alpha T} }{\alpha} \cdot \underline{ \left( \frac{b}{x} \right)^{{\bar \mu_0} - \sqrt{{\bar \mu_0}^2 + 2 \alpha}} } d \alpha = \\ &&\int\limits_0^T e^{-\frac{t}{2} {\bar \mu_0}^2 } \cdot \frac{1}{2 \pi \imath} \int\limits_{\imath {\mathbb R}- \cdots} e^{\frac{t}{2} \beta} \left( \frac{b}{x} \right)^{{\bar \mu_0} - \sqrt{\beta} } \frac{d \beta}{2} dt = \\ &&\int\limits_0^T e^{-\frac{t}{2} {\bar \mu_0}^2 } \cdot \left( \frac{b}{x} \right)^{{\bar \mu_0}} \cdot \frac{1}{2} \cdot e^{- \frac{(\log(\frac{b}{x}))^2}{2 t} } \cdot \frac{\log(\frac{b}{x})}{t^{3/2}} \cdot \sqrt{\frac{2}{\pi}} dt = \\ && \frac{1}{2} \left[ \text{erfc} \left( \frac{-{\bar \mu_0} T + \log(\frac{b}{x})}{\sqrt{2 T}} \right) + \left( \frac{b}{x} \right)^{2 {\bar \mu_0}} \cdot \text{erfc} \left( \frac{+{\bar \mu_0} T + \log(\frac{b}{x})}{\sqrt{2 T}} \right) \right] \tag{2} \end{eqnarray}
In the first line we just expressed the result through the Laplace transform. In the second line we took the limit $\theta \rightarrow 1_-$ by using the asymptotic expansions of the modified Bessel function of the first kind 10.41.3 in here. In the third line we substituted $\beta := {\bar \mu_0}^2 + 2 \alpha$. In the forth line we used the result from my first answer in here and in the last line we used the identity $\int \exp(-A t^2 - B t^{-2} ) dt = \frac{\sqrt{\pi } \left(e^{-2 \sqrt{A} \sqrt{B}} \left(1-\text{erf}\left(\frac{\sqrt{B}}{t}-\sqrt{A} t\right)\right)+e^{2 \sqrt{A} \sqrt{B}} \left(\text{erf}\left(\sqrt{A} t+\frac{\sqrt{B}}{t}\right)-1\right)\right)}{4 \sqrt{A}} $.
Now, the expression the last line is the cumulative density of the running supremum for the geometric Brownian motion, see here for example.
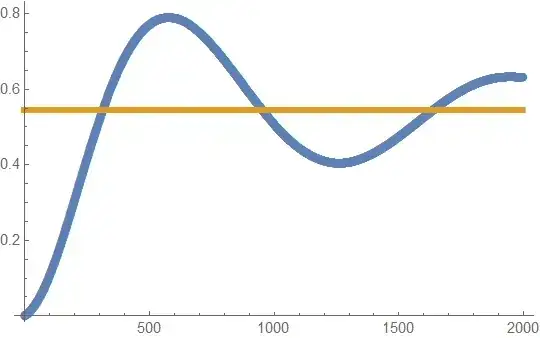
To be absolutely sure that there is no error in the above calculations we compare the expression $(1)$ with the last line $(2)$. We randomly selected $\mu_0,x,b$ then we took $\theta = 999/1000$ and we plot the cumulative sum of the first two thousand terms in the sum in $(1)$ (Blue) against the expression in the last line in $(2)$ (Yellow). As you can see there is a match.
(*The Bromwich integral versus the sum over the zeros of the Bessel \
function. All this in the limit theta --> 1_-.*)
numzrs = 2000; T = 3;
myInt[alpha_] :=
1/(2 Pi I) (-1 + Exp[alpha T])/
alpha (x/b)^(1/2 - mu0) BesselI[(mu0 - 1/2)/(1 - th),
x^(1 - th)/(1 - th) Sqrt[2 alpha]]/
BesselI[(mu0 - 1/2)/(1 - th), b^(1 - th)/(1 - th) Sqrt[2 alpha]];
(This is the limit of the above when theta -->1_-)
myIntinf[alpha_] :=
1/(2 Pi I) (-1 + Exp[alpha T])/
alpha (b/x)^(mu0b - Sqrt[mu0b^2 + 2 alpha]);
mu0 = RandomReal[{1/2, 1}, WorkingPrecision -> 50];
x = RandomReal[{1, 2}, WorkingPrecision -> 50];
b = RandomReal[{3 x, 10}, WorkingPrecision -> 50];
th = 999/1000;
mu0b = mu0 - 1/2;
nu = (1 - 2 mu0)/(2 (1 - th));
aa = N@Table[AiryAiZero[k], {k, 1, numzrs}];
myzrs = N[Table[BesselJZero[-nu, xi], {xi, 1, numzrs}], 15];
myzrs1 = N[
Table[(-nu) (1 - aa[[xi]]/2^(1/3) (-nu)^(-2/3)), {xi, 1, numzrs}],
15];
(The Bromwich integral)
(resinf=I NIntegrate[myIntinf[I
alpha],{alpha,-Infinity,Infinity},WorkingPrecision[Rule]15,
PrecisionGoal[Rule]12])
resinf = 1/
2 (Erfc[(-mu0b T + Log[b/x])/
Sqrt[2 T]] + (b/x)^(2 mu0b) Erfc[(mu0b T + Log[b/x])/
Sqrt[2 T]]);
(Sum over the residues.)
res1 = Accumulate[
Table[2 I (1 -
E^(-(1/2) b^(-2 + 2 th) T (1 - th)^2 myzrs[[xi]]^2)) (x/b)^(
1/2 - mu0)
BesselI[-nu,
I (x/b)^(1 - th)
myzrs[[xi]]]/((D[ BesselI[-nu, z], z] /.
z :> I myzrs[[xi]]) myzrs[[xi]]), {xi, 1, Length[myzrs]}]];
ListPlot[{res1, Re@resinf ConstantArray[1, {numzrs}]}, Joined :> True,
PlotMarkers -> Automatic, PlotRange -> All]
Second way:
Here, I would like to start from equation $(1)$ and use properties of Bessel functions only to get the limit in question.
Unfortunately,for the time being, I know too little about those things. However, naively, one could always take the Bessel function in the numerator and expand it in a Taylor series in $\theta$ about unity. This would then lead to the following identity:
\begin{eqnarray} I_{-\nu} \left[ (\frac{x}{b})^{1-\theta}\imath \zeta_\xi^{(-\nu)}\right] = \underbrace{I_{-\nu} \left[ \imath \zeta_\xi^{(-\nu)}\right]}_{0} + I_{-\nu}^{'} \left[ \imath \zeta_\xi^{(-\nu)}\right] \cdot (1-\theta) \log(x/b) (\imath \zeta_\xi^{(-\nu)}) + O(1-\theta)^2 \tag{3} \end{eqnarray}
Now, be inserting $(3)$ into $(1)$, we see that the denominator in $(1)$ cancels and as such the right hand side is proportional to $(1-\theta)$ and it disappears in the limit in question (note that the term in square brackets in $(1)$ has a finite limit due to the asymptotic behavior of the Bessel function zeros (see 10.21.41 in here) ) . This reasoning is obviously wrong.
Where is the error?