1

I was interested by this question in finding the volume of a solid of revolution using a "more accurate" cone frustum instead of the usual cylindrical disk.

So, starting with the volume of a cone frustum $ V = \frac{\pi}{3} ( R^2 + r^2 + Rr ) $, compute:

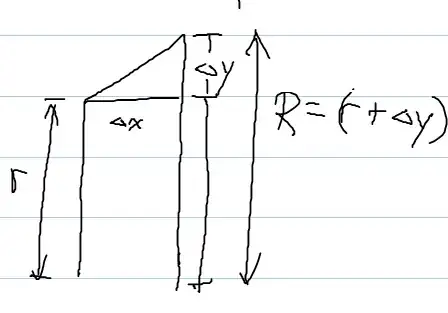conical frusta $$ \frac{\pi}{3}( (r+ \Delta y)^2 + r^2 + (r+ \Delta y)(r) ) \Delta x $$

$$ = \frac{\pi}{3}( 3r^2 + 3 r \Delta y + \Delta y^2 ) \Delta x $$

Which is interesting, because the regular disk formula comes out if you ignore the $ \Delta y $ terms, which means you're assuming the cone is actually a cylinder.

I'm not sure how to finish this though! How can I work with $ \Delta y $ to create an integral formula?

Community
  • 1
bobobobo
  • 9,502
  • Typically, you're working with the graph of some function so that, for instance, $r=f(x)$. This would make $r+\Delta y=f(x+\Delta x)$, so $\Delta y=f(x+\Delta x)-f(x)$. Now, if we go back to your final expression, $$\begin{align} \frac{\pi}{3}( & 3r^2 + 3 r \Delta y + \Delta y^2 ) \Delta x \ &= \frac{\pi}{3}( 3(f(x))^2 + 3 f(x) (f(x+\Delta x)-f(x)) + (f(x+\Delta x)-f(x))^2 ) \Delta x \ &=\frac{\pi}{3}(2f(x)f(x+\Delta x)+(f(x+\Delta x))^2+(f(x))^2)\Delta x \ &=\frac{\pi}{3}(f(x)+f(x+\Delta x))^2\Delta x \end{align}$$ but that seems wrong I'm not sure where to go from there. – Isaac Jun 20 '11 at 23:06
  • @Isaac: The 2 in the next to last line of your derivation should not be there. Compare the original volume formula. – Niels J. Diepeveen Jun 21 '11 at 00:07
  • @Niels: Ahh! Okay, so the end line could be written as $$\frac{\pi}{3}\left((f(x)+f(x+\Delta x))^2-f(x)f(x+\Delta x)\right)\Delta x,$$ which at least feels more plausible because it collapses to something very much like $\pi(f(x))^2;dx$ when $\Delta x\to 0$. – Isaac Jun 21 '11 at 00:14
  • @Nils your comment can be the answer – bobobobo Jul 19 '11 at 23:40

1 Answers1

1

Just assuming that $r$ varies continuously with $x$, you get that $\Delta y \to 0$ as $\Delta x \to 0$.

So in the limit you get $$ \frac{dV}{dx} = \lim_{\Delta x \to 0} \frac{\pi ( 3r^2 + 3 r \Delta y + \Delta y^2) \Delta x}{3 \Delta x} = \pi r^2 $$

Niels J. Diepeveen
  • 6,835