3

I need a series expansion at $x=0$ (with nth term please) for $$f(x)= \left(\frac{\sin x}{x}\right)^a$$ where $a>0$ is a real number.

We know that $$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-...$$

So we have $$\frac{\sin x}{x}=1-\frac{x^2}{3!}+\frac{x^4}{5!}-...$$

Now if we take $y= -\frac{x^2}{3!}+\frac{x^4}{5!}-...$ then $$\left(\frac{\sin x}{x}\right)^a=(1+y)^a$$ Then by Binomial theorem we have $$\left(\frac{\sin x}{x}\right)^a=1+a y+\frac{a(a-1)}{2!}y^2+ +\frac{a(a-1)(a-2)}{3!}y^3+... $$ Now I am stuck to calculate $y^2,y^3,...$

Another approach $$f(x)= \left(\frac{\sin x}{x}\right)^a$$ So on differentiation $$f'(x)=a \left(\frac{\sin x}{x}\right)^{a-1} \left(\frac{x\cos x-\sin x}{x^2}\right) $$ So we have taking the limit of above function as $x\to 0$ $$f'(0)=0$$

This is again where I am stuck. Any help would be surely appreciated. Thank you.

Max
  • 536

1 Answers1

6

We start with the power series expansion of the sinc function given by $$ \operatorname{sinc}x=\frac{\sin x}{x}=\sum_{k=0}^\infty\frac{(-1)^k}{(2k+1)!}x^{2k}. $$ To obtain a series expansion for powers of the sinc function we may use this formula to write $$ \tag{1} \operatorname{sinc}^ax=\sum_{m=0}^\infty c_m x^{2m}, $$ where $c_0=1$ and the higher-order coefficients obey the recursive relation $$ c_m=\frac{1}{m}\sum_{k=1}^m(ka-m+k)\frac{(-1)^k}{(2k+1)!}c_{m-k}. $$ The series expansion given by $(1)$ has been tested for integer and noninteger values of $a$ on the interval $(-\pi,\pi)$. For $a\in\Bbb N$ this expansion should converge on all of $\Bbb R$.

To implement in Mathematica we may define the coefficients $c_m$ as follows:

f[x_, a_] := Sinc[x]^a;
c[0, a_] := 1;
c[m_, a_] := 1/m Sum[(k a - m + k) (-1)^k/(2 k + 1)! c[m - k, a], {k, 1, m}];
g[x_, a_, M_] := Sum[c[m, a] x^(2 m), {m, 0, M}];

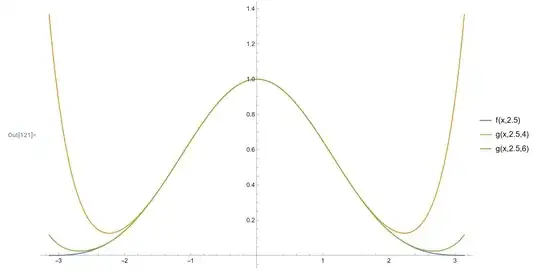
As an example, here is a plot comparing $f(x,a)=\operatorname{sinc}^ax$ to the series expansion $g(x,a,M)$ for $a=2.5$ and $M=4,6$ showing the expansion converging to the target function as the number of terms increases. Example Plot

Finally, here is a table of the first eleven coefficients $c_m$: $$ \left( \begin{array}{cc} m & c_m \\ 0 & 1 \\ 1 & -\frac{a}{6} \\ 2 & \frac{1}{360} a (5 a-2) \\ 3 & -\frac{a (7 a (5 a-6)+16)}{45360} \\ 4 & \frac{a (5 a-4) (7 a (5 a-8)+36)}{5443200} \\ 5 & -\frac{a (11 (a-2) a (35 (a-2) a+104)+768)}{359251200} \\ 6 & \frac{a (13 a (77 a (5 a (35 (a-6) a+572)-4248)+255968)-1061376)}{5884534656000} \\ 7 & -\frac{a (a (13 a (77 a (5 a (a (5 a-42)+164)-1848)+190112)-1810176)+552960)}{35307207936000} \\ 8 & \frac{a (17 a (a (13 a (385 a (5 a (a (5 a-56)+296)-4672)+3586192)-57567616)+39964416)-200005632)}{144053408378880000} \\ 9 & -\frac{a (19 a (17 a (7 a (13 a (385 a (a (5 a (5 a-72)+2472)-10368)+10994448)-260572032)+2116182272)-23881992192)+129369047040)}{1034591578977116160000} \\ 10 & \frac{a (a (209 a (17 a (7 a (325 a (55 a (a (35 (a-18) a+5448)-29232)+5815248)-4716438048)+56126325760)-1051637137920)+140441050828800)-38930128699392)}{3414152210624483328000000} \\ \end{array} \right) $$

Gary
  • 31,845
Aaron Hendrickson
  • 6,042
  • As far as I know, formulas like $(1+x)^a = 1+ax+\frac{a(a-1)}{2}x^2 + \cdots$ works for any real $a$ too - I think it works for complex $a$ too, so I'm definitely not surprised that the same formula for power series works here. – Gareth Ma Mar 04 '23 at 19:16
  • @GarethMa Also worth noting is $\operatorname{sinc}x$ is positive near $x=0$ when $\operatorname{sinc}x$ is negative, the expansion for noninteger $a$ gives the completely wrong answer. – Aaron Hendrickson Mar 04 '23 at 19:19
  • Is your formula also true for any real number $a>0$? – Max Mar 05 '23 at 01:27
  • @Max Yes. For noninteger $a$ it appears to converge on $(-\pi,\pi)$. – Aaron Hendrickson Mar 05 '23 at 01:29
  • Thank you so much.+1 for your beautiful answer. Can we simplify the $c_m$'s a little bit please. – Max Mar 05 '23 at 01:31
  • 1
    @AaronHendrickson If $a$ is not a non-negative integer, $(\sin x/x)^a$ will be singular at $\pm \pi$, hence the radius of convergence is indeed $\pi$. – Gary Mar 05 '23 at 23:16
  • @Gary Thanks. I had suspected so. For nonegative integer $a$ the radius of convergence should be infinite correct? – Aaron Hendrickson Mar 05 '23 at 23:46
  • @AaronHendrickson Yes since $\sin x/x$ and any polynomial are entire functions. – Gary Mar 06 '23 at 00:11
  • I have accepted your answer. I would really appreciate if you could simplify $c_m$ a bit please. – Max Mar 07 '23 at 07:26
  • @Max I tried to find a closed-form for the coefficients but was unsuccessful. What I would suggest is post another question to the site specifically about a simplified form for the coefficients. Provide a link in the new question back to this one so that people understand the context/motivation for the follow up post. – Aaron Hendrickson Mar 07 '23 at 09:07
  • Ok thank you a lot – Max Mar 07 '23 at 09:40