Inequalities - Absolute Value $|2x-1| \leq |x-3|$

Question

$$|2x-1| \leq |x-3|$$

Answer is $$-2 \leq x \leq \frac43$$

My Question is HOW?

Can someone explain to me how please? – MATHSUSER Aug 05 '13 at 07:12 — MATHSUSER, Aug 05 '13 at 07:12

score 6 · Accepted Answer · answered Aug 05 '13 at 07:19

6

There are $3$ cases to consider.

Case 1: Suppose $x<\frac{1}{2}$. Then we obtain: $$ -(2x-1) \leq -(x-3) \iff -2x+1 \leq -x+3 \iff -2 \leq x $$ So for this case, we know that $\boxed{-2 \leq x < \dfrac{1}{2}}$ will be part of our solution.

Case 2: Suppose $\frac{1}{2} \leq x \leq 3$. Then we obtain: $$ +(2x-1) \leq -(x-3) \iff 2x-1 \leq -x+3 \iff 3x \leq 4 \iff x\leq \dfrac{4}{3} $$ So for this case, we know that $\boxed{\dfrac{1}{2} \leq x\leq \dfrac{4}{3}}$ will be part of our solution.

Case 3: Suppose $x>3$. Then we obtain: $$ +(2x-1) \leq +(x-3) \iff 2x-1 \leq x-3 \iff x \leq -2 $$ But this contradicts the fact that $x>3$, so we reject this part of the solution.

Combining the other two cases together, we obtain: $$ \boxed{-2 \leq x\leq \dfrac{4}{3}} $$ as desired.

answered Aug 05 '13 at 07:19

Adriano

41,576

The 1/2 and 3 are the answers I achieved, however I don't understand how you apply to the question again with the + and - – MATHSUSER Aug 05 '13 at 07:22
Oh, Nevermind I Understand thank you! – MATHSUSER Aug 05 '13 at 07:24
2

Recall that: $$ |f(x)| = \begin{cases} +f(x) & \text{if }f(x) \geq 0 \ -f(x) & \text{if }f(x) < 0 \ \end{cases}$$ So, for example, I could replace $|2x-1|$ with $-(2x-1)$ in Case 1 because if $x<\frac{1}{2}$, then $2x-1<0$. – Adriano Aug 05 '13 at 07:25

Mahdi Khosravi · Answer 2 · 2013-08-05T08:36:13.843

As it is shown in this plot :

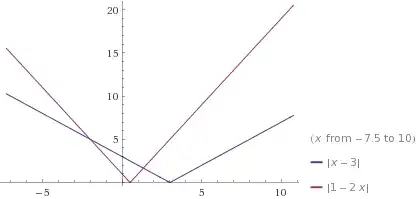
enter image description here

You can divide the $x$ values into these parts:

$x<\frac12$ , $\frac12 < x < 3$ , and $x>3$ and get the answer which is the way Adriano answered too.

Another way is squaring two sides :

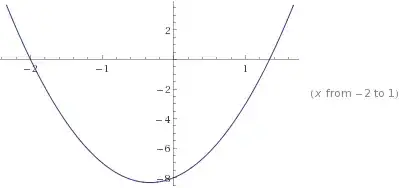
$ |2x-1|^2 \leq |x-3|^2 \Rightarrow 3x^2+2x-8 \leq 0 $ Now let's find the roots and then find the values in which function is not positive. $ 3x^2+2x-8 = 0 \Rightarrow x = \frac{-2 \pm\sqrt{(-2)^2-4\times3\times(-8)}}{2\times3} = \begin{cases}{-2\\ \frac43} \end{cases}$

So this points are zeros of function and since the function is differentiable we can conclude that in this points the sign of the function changes. And it is easy to find that for $(-\infty , -2) \cup(\frac43, +\infty) $ function is positive and for $[-2 , \frac43]$ it is not positive (As it is shown in the below figure) enter image description here

But how does this come the the answer? -2 <=x <= 4/3 (sorry if i sound stupid) because i can see it on the graph, but how do i prove this from the inequality? — MATHSUSER, Aug 05 '13 at 07:14

score 1 · Answer 3 · answered Aug 05 '13 at 10:52

Another purely algebraic approach without breaking it into cases from the beginning:

$$|2x-1|\le|x-3|\stackrel{\text{square sides}}\iff 4x^2-4x+1\le x^2-6x+9\iff3x^2+2x-8\le0\;\;(**)$$

Let us try now to factor the left side:

$$ \Delta=4+96=100\implies x_{1,2}=\frac{-2\pm 10}{6}=\begin{cases}-2\\{}\\\frac43\end{cases}$$

so

$$(**)\;\;\;3(x+2)\left(x-\frac43\right)\le 0\iff -2\le x\le\frac43$$

Inequalities - Absolute Value $|2x-1| \leq |x-3|$

3 Answers3

Linked