What are the steps to solving $|3x + 1| > |2x - 7|$ with the given answer as $(-∞,-8)\cup(6/5,∞)$?
I am having difficulty with understanding inequalities with absolute value functions on both sides, what are the steps for solving this example problem?
HINT:
As for real $x, |x|=+x$ if $x\ge0$ and $-x,$ if $x<0$
Check for $3x+1<=>0$ and $2x-7<=>0$
To add to lab's response, a useful trick is to draw a picture of the real line. On it, indicate the critical points at which your absolute value functions switch signs. (In this case, those points are $-\frac{1}{3}$ and $3.5$.) Now, consider the various cases where $x$ may be located on that real line.
For example, for $x\geq 3.5$ (i.e. $x$ lies on or to the right of the point $3.5$), then $|3x+1|=3x+1$ and $|2x-7|=2x-7$ so you have $$ 3x+1>2x-7\implies x>-8 $$ which is already satisfied for all $x\geq 3.5$. So $x\geq 3.5$ works. Now you move on to the next case (e.g. $-\frac{1}{3}\leq x<3.5$).
EDIT: fine, a bit more details: now that we have established $x\geq 3.5$ works, consider $-\frac{1}{3}\leq x<3.5$. In this case, $|3x+1|=3x+1$ and $|2x-7|=7-2x$ so $$ 3x+1>7-2x\implies 5x>6\implies x>\frac{6}{5}. $$ So if $-\frac{1}{3}\leq x<3.5$, you want $x>\frac{6}{5}$. In other words, $x\in(\frac{6}{5},3.5)$ works.
Finally, consider $x<-\frac{1}{3}$. Then, $|3x+1|=-3x-1$ and $|2x-7|=7-2x$ so $$ -3x-1>7-2x\implies x<-8. $$ So you want $x\in(-\infty,-\frac{1}{3})\cap(-\infty,-8)=(-\infty,-8)$.
Putting all cases together, the solution set is $$ (-\infty,-8)\cup(\frac{6}{5},3.5)\cup[3.5,\infty)=(-\infty,-8)\cup(\frac{6}{5},\infty). $$ All this is a lot easier if you have a picture while following it.
EDIT 2: another visual aid for simple cases like this is to plot both the left hand side and right hand side. This is another way to make sure you understand how the absolute value function works. You should get something like this:
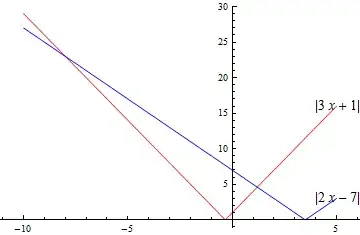
Now, you are interested in the values of $x$ where the red line is above the blue line.
In this case you could also use the fact that $|a|^2=a^2$.
The original inequality $$|3x+1|>|2x-7|$$ is equivalent to $$(3x+1)^2>(2x-7)^2.$$ (Since both sides are positive, squaring gives an equivalent inequality. This would not be true for arbitrary inequality.)
Now with some manipulation you should be able to get $$5x^2+34x-48=5(x^2+\frac{34}5x-\frac{48}5)>0$$ and then solve this quadratic inequality.
The same approach was used in this answer and this answer to a similar question.
