In a composition of two inversions, characterize straight lines that remain straight lines

Question

Let S1 and S2 be the inversions in the circles $x^2+y^2 = 16$ and $(x−8)^2+y^2 = 1$ respectively. Consider the composition W for these inversions W = T2 ◦T1. Which lines under the transformation W will become lines?

From my knowledge, I know that lines are inverted to lines when they pass through the center of the circles of inversion. So for the line to remain lines under inversion does the non-inverted line have to pass through the centers of both the circles above? Is that the only way it remains a line?

Answer 1

Circles and lines mapped to lines by circle inversion are exactly those which pass through the center of inversion; the center is the only point mapped to infinity. However, inversion is a bijection so there is exactly one point that $S_1$ maps to the center of $S_2$. It is the point on the line between the centers of $S_1$ and $S_2$ a distance $d$ from the center of $S_1$ such that $$ 8d = 16 \implies d = 2 $$ since the center of $S_2$ is 8 units away from the center of $S_1$ and 16 is the squared radius of $S_1$. This point has coordinates $(2, 0)$. The set of all lines which map to lines under $S_2\circ S_1$ is exactly all lines which pass through this point. Note that the radius of $S_2$ is irrelevant.

Answer 2

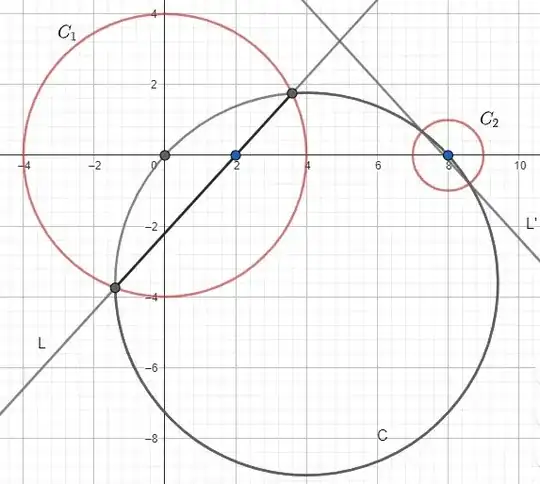
Fig. 1: $\textit{The image of line L by the first inversion is circle C}.$ $\textit{As this circle passes through the center of the second inversion,}$ $\textit{it is transformed into line L'.}$

Here is an answer using complex representation of inversions.

(refer to this site and/or this question of mine for explanations)

$$z \xrightarrow{ \ \ \ T_1 \ \ \ } \underbrace{\frac{16}{\overline{z}}}_{T_1(z)}=\zeta\xrightarrow{ \ \ \ T_2 \ \ \ } \underbrace{8+\frac{1}{\overline{\zeta}-8}}_{T_2(\zeta)}=Z$$

giving by composition:

$$Z=\underbrace{8+\frac{z}{16-8z}}_{T_3(z):=T_2 \circ T_1(z) }$$

with inverse transform

$$z=\frac{16 Z - 8}{8Z - 63}\tag{1}$$

Now let us recall the general equation of a "cline", a term used in the first reference I gave above for encompassing at the same time a circle or a straight line in the complex plane :

$$Az\overline{z}+\overline{B}z+B\overline{z}+C=0 \ \text{with} \ A,C \in \mathbb{R}\tag{2}$$

• if $A \ne 0$, it is a circle.

• if $A=0$, it is a straight line ; in this case $B=\alpha+i\beta$ gives a normal vector $\binom{\alpha}{\beta}$ to the line.

Consider now a straight line $L$ with equation:

$$\overline{B}Z+B\overline{Z}+C=0 \ \text{with} \ C \in \mathbb{R}\tag{3}$$

Let us see the constraint that must be placed on its coefficients $B$ and $C$ for having an image $L'$ which is itself a straight line.

The equation of $L'$ will be obtained by plugging relationship (1) into (3). If we reduce to a same denominator, we will get the equation of a cline with a term $k Z\overline{Z}$. This cline will be a line if and only if coefficient $k$ is $0$.

A little calculation shows that this condition is equivalent to:

$$128(\overline{B}+B)+64C=0 \ \iff \ C=-2(B+\overline{B})$$

which means, using (3), that the equation of the line must be:

$$\overline{B}(z-2)+B\overline{(z-2)}=0 \ \text{for any } \ B$$

which is the general equation of a line passing through point $z=2+0i$.

We find back in this way the result of Nicholas.