I don't have a copy of Apostol at hand, but I guess he is using this as an example of the general fact that we are not always allowed to change the order of two limit processes. Here $D$ and $n\to\infty$ in
$$D(\lim_{n\to\infty} f_n(x))=\lim_{n\to\infty} D(f_n(x)).\qquad(*)$$
I'm sure Apostol explains somewhere that a suitable extra condition (like the sequence of derivatives $f_n'(x)$ converging uniformly) does allow the change of the order here.
For a bit of extra we can look at the situation at $x=0$ specifically by plotting a few of the functions from the sequence.
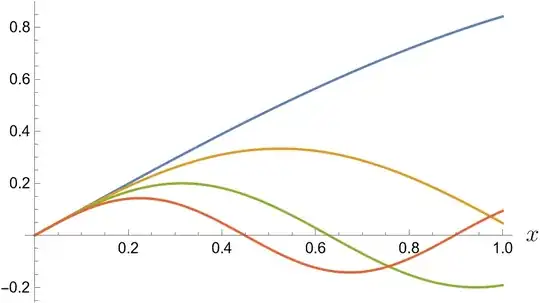
In the image you see the graphs of $f_1,f_3,f_5$ and $f_7$. You see that near $x=0$ they have nearly identical slopes. That's exactly because $f_n'(0)=1$ for all $n$. But you also see that the graphs follow this tangent line for shorter and shorter intervals before they begin to oscillate.
You may also consider the following. Let's look at the sequence of functions
$$f_n(x)=\frac1n\sin(nx+\alpha_n),$$
where $\alpha_n$ is a random phase shift. We still have $f_n\to 0$ uniformly. Only this time $f'_n(x)=\cos(nx+\alpha_n)$ need not even converge to anything anywhere (not at any $x$).
Or even
$$f_n(x)=\frac1n\sin(n^2x).$$
We still have $f_n\to0$ uniformly (the factor $1/n$ is decisive). This time
$$f'_n(x)=n\cos(n^2x),$$
and $f'_n(0)\to\infty$ as $n\to\infty$.
See below for the sample plots $f_1,f_3,f_5,f_7,f_9$ from this sequence.
Observe that as $n\to\infty$ the derivatives at zero $\to\infty$, the sine waves become steeper and steeper.

The point (if any) is that in general uniform convergence of a sequence itself does not say anything about the convergence of the derivatives. The power series form a notable exception, and in the case of power series we are always guaranteed that the sequence of derivatives also converges uniformly (on any compact interval contained in the interval of convergence). As we saw, a sequence of wildly oscillating ($\Rightarrow$ larger and larger derivatives) functions can converge to zero uniformly.
A sine wave can be as steep as we desire without the amplitude going up, simply increase the frequency. The amplitudes tending to zero gives uniform convergence of the functions, and this is unrelated to how steep the waves become because the frequency can (over)compensate.
The general problem requiring adjustments in one's intuition really is about mixing two limit processes. This may become clearer if, instead of $D$ we think of the derivative as the limit of a sequence. Like
$$
f'(x)=\lim_{m\to\infty}\frac{f(x+\frac1m)-f(x)}{1/m},\qquad(**)
$$
something that holds when $f$ is differentiable at $x$. Rewritten like this
the question is whether
$$
\lim_{n\to\infty}\left(\lim_{m\to\infty}\frac{f_n(x+\frac1m)-f_n(x)}{1/m}\right)\stackrel{?}{=}\lim_{m\to\infty}\left(\lim_{n\to\infty}\frac{f_n(x+\frac1m)-f_n(x)}{1/m}\right).
$$
Superficially it looks like it could hold more generally, but you have encountered similar problems earlier. Compare with something from a first course on limits of sequences of numbers:
$$
\lim_{n\to\infty}\lim_{m\to\infty}(1+\frac1m)^n=\lim_{n\to\infty}1^n=1,
$$
but
$$
\lim_{m\to\infty}\lim_{n\to\infty}(1+\frac1m)^n=\lim_{m\to\infty}\infty=\infty,
$$
and
$$
\lim_{n\to\infty}(1+\frac1n)^n=e.
$$
Combinations of limit processes are nuanced. Among other things the order in which the limits are taken may play a role.
After this excursion one begins to appreciate "obvious" results like:
Theorem. If the limits $\lim_{n\to\infty}a_n=A$ and $\lim_{n\to\infty}b_n=B$ with both $A$ and $B$ real numbers (so finite) exist, then
$$
\lim_{n\to\infty}\lim_{m\to\infty} a_nb_m=
\lim_{m\to\infty}\lim_{a\to\infty} a_nb_m=
\lim_{n\to\infty}a_nb_n=AB.
$$
The content of this theorem being that under these circumstances we actually can do the limits of $(a_n)$ and $(b_n)$ separately, and in any which order we prefer.

