This question involves both math and programming, but the main inquiry in nature is mathematical.
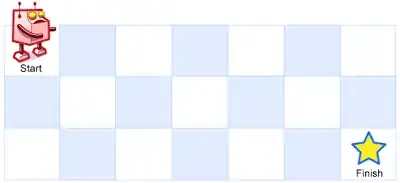
There is a LeetCode question called Unique Paths that asks the number of ways that one can reach the lower-right corner of a $m \times n$ grid if you start in the upper-left corner and want to reach the lower-right corner, only being able to move down or right at any step.
Visualization of the $3 \times 7$ case, for example:
One mathematical approach that was suggested is to compute $\begin{pmatrix}m + n - 2 \\ m - 1\end{pmatrix}$ as the question is equivalent to asking the number of ways to select $m - 1$ downwards moves from a total of $m + n - 2$ moves to reach the lower-right corner.
However, the programming solution that was proposed essentially computes the following:
$$ \left\lfloor \frac{\left\lfloor \frac{\left\lfloor \frac{\left\lfloor \frac{1 \cdot n}{1} \right\rfloor (n + 1)}{2} \right\rfloor (n + 2)}{3} \right\rfloor \cdots (n + m - 2)}{\vdots \atop m - 1} \right\rfloor $$
So, my question is how does the solution guarantee that the above is equivalent to $\left\lfloor \frac{(m + n - 2)!}{(m - 1)!(n - 1)!} \right\rfloor$ without any loss of data from the repeated application of the floor operator?
Edit:
The accepted answer from Sil helped me out the most intuitively. Though, the inductive proof of how each step results in a combination by Mike also helped very much.