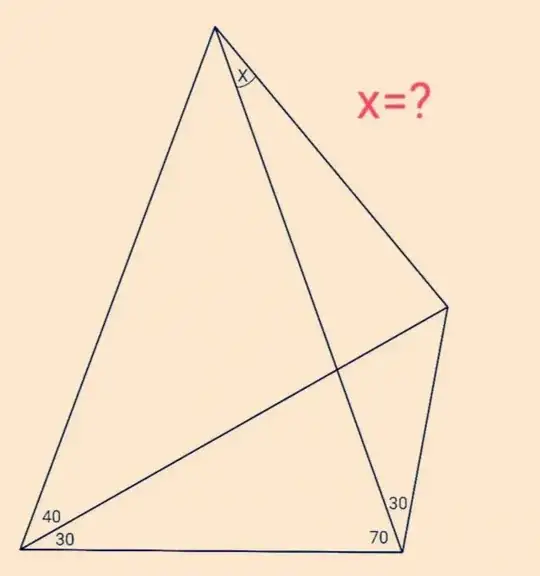
Fairly simple question, in my opinion. Below is a given quadrilateral $ABCD$ and the goal is to solve for the angle labeled $x$ in the diagram. I'm going to post my own approach as an answer. I'm unsure if my solution or my answer are correct, or if there are other better ways to arrive at an answer. Please share your solutions as well!
Your solution looks correct to me.
I'm going to write two solutions.
Solution 1 :
Let us take $E$ such that $\triangle{ACE}$ is an equilateral triangle. ($E$ is on the same side of $AC$ as $D$.)
Now, let us first show that $B,D,E$ are collinear.
Since $AB=AC=AE$, we see that $\triangle{ABE}$ is an isosceles triangle, and so we get $$\angle{ABE}=\frac{1}{2}(180^\circ-\angle{BAE})=\frac{1}{2}(180^\circ-100^\circ)=40^\circ=\angle{ABD}$$ Therefore, it follows that $B,D,E$ are collinear.
Since $\triangle{DCA}$ is congruent to $\triangle{DCE}$, we obtain $$x=\angle{DAC}=\angle{DEC}=\color{red}{20^\circ}$$
Solution 2 :
This is a trigonometric approach.
Using the law of sines in $\triangle{ABD}$, we have $$AD=\frac{\sin 40^\circ}{\sin(100^\circ-x)}AB\tag1$$ Using the law of sines in $\triangle{ADC}$, we have $$AD=\frac{\sin 30^\circ}{\sin(150^\circ-x)}AC\tag2$$
From $(1)(2)$ with $AB=AC$, we get $$\frac{\sin 40^\circ}{\sin(100^\circ-x)}=\frac{\sin 30^\circ}{\sin(150^\circ-x)}$$ i.e. $$\sin 40^\circ\ \bigg(\frac 12\cos x+\frac{\sqrt 3}{2}\sin x\bigg)=\frac 12(\sin 100^\circ\cos x-\cos 100^\circ\sin x)$$
Dividing the both sides by $\frac 12\cos x$, and solving it for $\tan x$ give $$\begin{align}\tan x&=\frac{\sin 100^\circ-\sin 40^\circ}{\sqrt 3\sin 40^\circ+\cos 100^\circ} \\\\&=\frac{\sin(90^\circ +10^\circ)-\sin(30^\circ+10^\circ)}{\sqrt 3\sin(30^\circ+10^\circ)+\cos(90^\circ +10^\circ)} \\\\&=\frac{\frac 12\cos 10^\circ-\frac{\sqrt 3}{2}\sin 10^\circ}{\frac{\sqrt 3}{2}\cos 10^\circ+\frac 12\sin 10^\circ} \\\\&=\frac{\frac{1}{\sqrt 3}-\tan 10^\circ}{1+\frac{1}{\sqrt 3}\tan 10^\circ} \\\\&=\frac{\tan 30^\circ -\tan 10^\circ}{1+\tan 30^\circ \tan 10^\circ} \\\\&=\tan (30^\circ -10^\circ) \\\\&=\tan 20^\circ\end{align}$$ Therefore, we get $x=\color{red}{20^\circ}$.
So, this is my approach to this problem, I'll add an explanation as well:
This is the procedure I followed:
1.) Label the Quadrilateral as $ABCD$. Mark all the given angles, equal sides as well as some basic angles that can be chased.
2.) Locate the circumcenter of $\triangle BCD$ inside $\triangle ABC$ and label it point $E$. Connect all the vertices of $\triangle BCD$ to circumcenter $E$ such that segment $BE=EC=CD=DE$. Also connect point $A$ with $E$ via segment $AE$ . Notice that this means $\triangle ECD$ is equilateral, which implies $\angle ECA=30$. It follows that $\triangle AEC$ is congruent to $\triangle ADC$ via the SAS property. This means that $\angle EAC$ is also $x$.
3.) Lastly, notice that $\triangle AEB$ is also congruent to $\triangle AEC$ (and $\triangle ADC$) via the SAS property as well. This also means that $\angle EAB$ is $x$ as well. Thus, via the angle sum property, we can establish that $2x+70+70=180$, therefore $x=20$.
In 3.) We already knew that $\angle BAC=40^{\circ}$ so $2x=40^{\circ}$.
Lebeling the vertices $A,B,C,D$ starting from the vertex of the angle $x$, and the interior angles as $a_2=x,a_1=40^{\circ},b_2=40^{\circ},b_1=30^{\circ},c_2=70^{\circ}, c_1=30^{\circ}, d_2=50^{\circ}, d_1=100^{\circ}-x$ counter clock-wise we have $$\frac{\sin a_2}{\sin a_1}\frac{\sin b_2}{\sin b_1}\frac{\sin c_2}{\sin c_1}\frac{\sin d_2}{\sin d_1}=1$$ $$\frac{\sin x}{\sin 40^{\circ}}\frac{\sin 40^{\circ}}{\sin 30^{\circ}}\frac{\sin 70^{\circ}}{\sin 30^{\circ}}\frac{\sin 50^{\circ}}{\sin(100^{\circ}-x)}=1$$ $$\sin(100^{\circ}-x)=4\sin50^{\circ}\sin70^{\circ}\sin x$$ $$\sin(100^{\circ}-x)=2\cos40^{\circ}(2\cos20^{\circ}\sin x)$$ $$x=20^{\circ}.$$
