7

I have some function, say, Gauss PDF

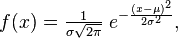
enter image description here

Now I want it to repeat, say, every N units

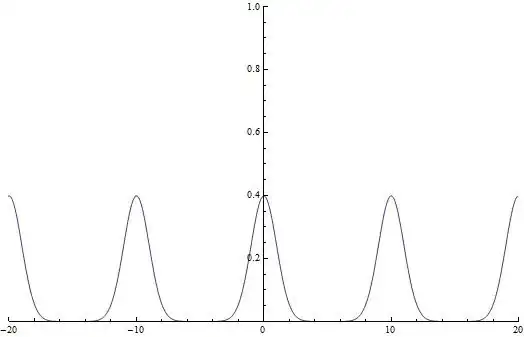
enter image description here

How to transform any function this way?

I know I can sum function at each shift. But is it possible to convert argument only? I.e. apply some transform to $x$ only?

UPDATE

Ideally, I would like to find $g_T(t)$ such that

$\sum\limits_{n=-\infty}^{\infty}F(t+nT) = F(g_T(t))$

where $n \in Z$, $F$ is any function and $T$ is desired period.

I don't know if it is possible in principle, for example, endless summing may produce infinities everywhere. In this case one may introduce some weighting in lefthand side...

UPDATE 1

My be lefthand size should be

$\lim\limits_{k \to +\infty}\frac{1}{2k}\sum\limits_{n \in Z}F(t+nT)$

Suzan Cioc
  • 931
  • The thing you now want is impossible as stated in the equation because (for positive $F$ like your Gaussian) the left hand side takes on values larger than $F$ at any single point. – not all wrong Jul 29 '13 at 09:30
  • i haven't read everything here carefully, but i feel like people here have made this issue more complicated than it needs to be. all you need is restrict $x$ to be between 0 and $T$, and define your function as $f(x+iT)=f(x)$ for all integers $i$ and an arbitrary period $T$. – abcd Oct 20 '15 at 01:26
  • ^ that should be "all you need is to restrict . . ." – abcd Oct 20 '15 at 01:43

2 Answers2

12

If you say $$p(x) = f(x\bmod N)$$

then $p$ is a periodic function with period of $N$, which has $p(x)=f(x)$ for all $x$ in $[0, N)$.

To make $p$ and $f$ agree on an interval that is symmetric around 0, you can use $$p(x) = f\left(\left(\left(x + \frac N2\right)\bmod N\right) - \frac N2\right)$$

which is again a function that has a period of $N$, but this time $p(x) = f(x)$ for all $x$ in $\left[-\frac N2, \frac N2\right)$.

If that's not what you want, please clarify what your question is.

MJD
  • 65,394
  • 39
  • 298
  • 580
  • These solutions effectively multiply the original function be a rectangular window before summing the function at each shift. More generally, you could use some other window function. For example, a smoother window would help to smooth out any discontinuities. In a way, this is a family of hybrid solutions between Suzan's and yours. – Chris Culter Jul 28 '13 at 19:59
  • So perhaps my answer isn't really pertinent? – MJD Jul 28 '13 at 20:02
  • Oh, I think your answer is extremely pertinent! It answers the original question: "But is it possible to convert argument only?" Using a non-rectangular window would mean doing more than just changing the argument to $f$. – Chris Culter Jul 28 '13 at 20:08
  • @ChrisCulter you could say that this means changing the argument to the "sawtooth curve" $x \pmod{n}$ – Ben Grossmann Jul 28 '13 at 20:12
  • 1
    @Omnomnomnom Yes, sorry, I should be clearer. I'm agreeing that MJD's answer is a positive solution to the question. My idea, on the other hand, breaks the rule by summing up a nonzero multiple of $f$ at more than one argument. – Chris Culter Jul 28 '13 at 20:15
  • Thanks for clarifying. I feel like I don't understand the context of the original question very well, so I wasn't at all sure that my answer would be useful. – MJD Jul 28 '13 at 21:12
  • @MJD I was thinking about this way. But this way I cut all values outside period, i.e. if function is not localized, that periodic version will notably differ. – Suzan Cioc Jul 29 '13 at 08:57
2

A possible approach is to use a Fourier series expansion of the function.

Suppose that you want to repeat the function $f(x)$ on the interval $[-L,L]$ where $L=N/2$, with $N$ as specified in the OP.

The fourier series expansion from this interval is $$ f(x)=a_0+\sum\limits_{n=1}^\infty a_n\cos\left(\frac{n\pi x}{L}\right)+b_n\sin\left(\frac{n\pi x}{L}\right), $$ where $$\begin{align} a_0&=\frac1{2L}\int_{-L}^Lf(x)\,dx,\\ a_n&=\frac1{L}\int_{-L}^Lf(x)\cos\left(\frac{n\pi x}{L}\right)\,dx,\text{ and}\\ b_n&=\frac1{L}\int_{-L}^Lf(x)\sin\left(\frac{n\pi x}{L}\right)\,dx. \end{align}$$

Given that your function $f$ is even, we will have $b_n=0$ for all $n$.

These integals do not appear to be expressible in terms of ordinary functions (see WolframAlpha). Thus, for this approach, the integrals have to be numerically approximated, which could cause further numerical problems.

Daryl
  • 5,598