Context
I'm making a 2D sci-fi game, and I've convinced myself that it would be neat to have player positions described in reference to nearby stars rather than using some kind of coordinate system. Realistically, the player would not have any way to measure its distance to nearby stars, but it could measure angles between nearby stars.
Problem
You would need to use at least 3 nearby stars to identify the Player's location, but just any old 3 stars are not sufficient. Under certain conditions, the 3 angles between the Player and each of the 3 stars can represent 2 points.
Here the red circles are the 3 stars, the pink circle is the Player, and the Yellow circle is a degenerate point. The arcs show all of the points (with some error margin) that can be represented by just a single angle (ie. The green arcs show all the possible positions that have the same angle Star 2 - Player - Star 3).
Keeping the same star positions, you can manipulate the player position to find an arangement that does not produce a degenerate point.
(Here is the janky jsfiddle I made that generates these images. Re-run to randomize the star positions, click to move the player position to the mouse position. This is not precise nor efficient, but serves to provide a visual aid)
Question
How could I compute whether or not a given relationship produces a degenerate point?
Or perhaps more relevant to my problem: Given a set of nearby stars, how could I select 3 stars such that the angles produced resolve to exactly 1 point in space?
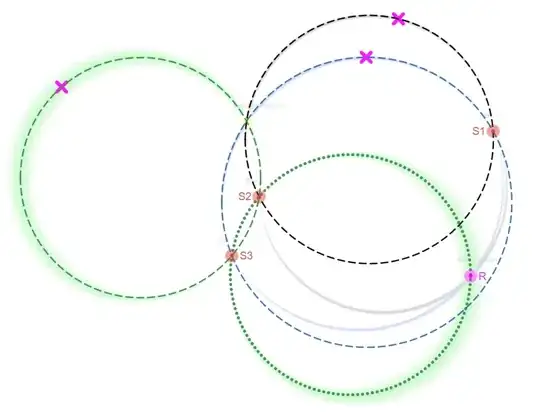

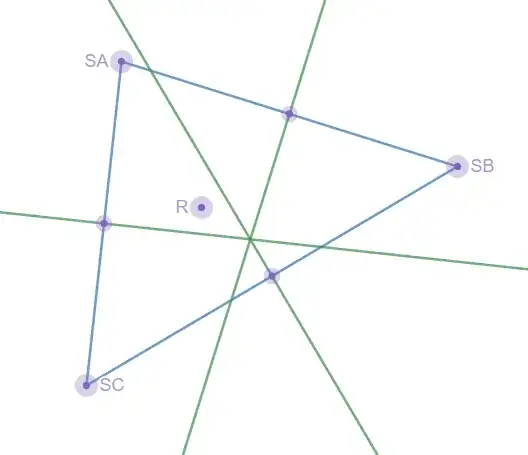
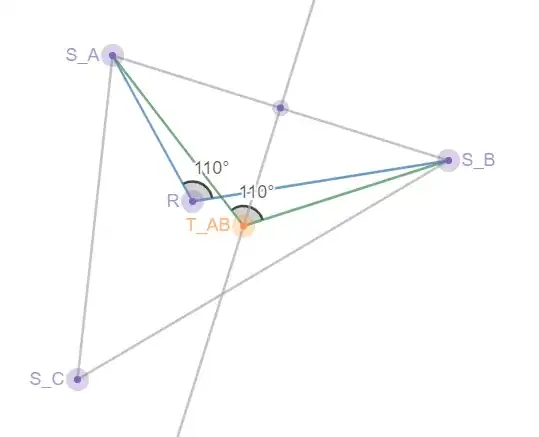

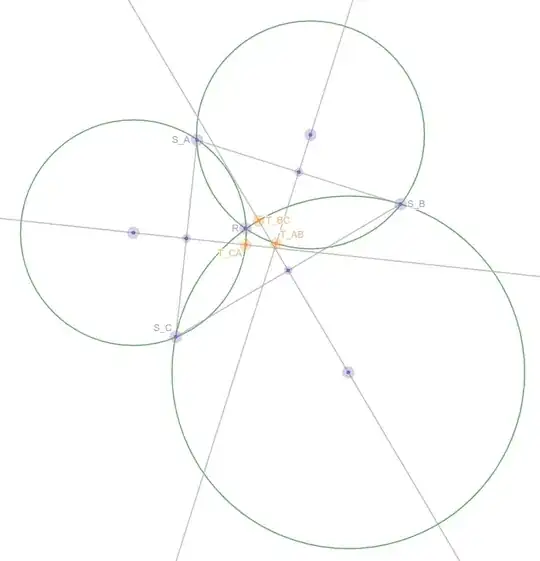
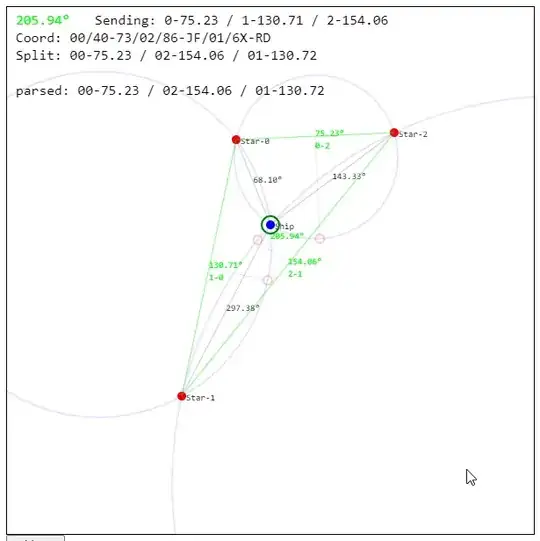
A straight line is also clearly not the only degenerate case, as the example image I provided shows 3 stars not in a straight line that still produce a degenerate point.
– Sunlis Jul 13 '22 at 22:38