0

For example, if you look at a soccer ball through a microscope, you can see a large irregular surface, while on a soccer field it looks like a point.

On the microscopic scale, carbon nanotubes have a three-dimensional structure, while on the macroscopic scale, carbon nanotubes can be seen as a curve.

The British coastline is microscopically fractal, on a world map, it is jagged, and in outer space, it is just a dot.

If a bald person grows a hair, from a distance he remains a bald person, but up close you can see that he has a hair. (This is somewhat similar to the fact that P(man=bold)=1 holds almost everywhere)

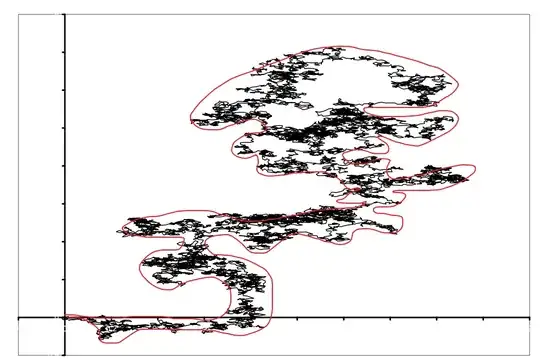
A trajectory of Brownian motion has a fractal structure and is irregular, but from a macroscopic point of view, its trajectory can be seen as a curve with a certain trend and a specific profile. enter image description here

When we measure the same thing with different scales, we can see different phenomena.

What branch of mathematics is about scale problems?

nevermind_15
  • 589
  • 4
    Regarding Brownian paths, I believe that you are incorrect: they satisfy the same irregularities at all scales. – Lee Mosher Jun 27 '22 at 14:48
  • @LeeMosher in the image I upload, I can draw an outline of the path, which in my eye is Determined. What I mean is, that I see more regular shapes at a certain scale. – nevermind_15 Jun 27 '22 at 15:12
  • And if you zoom in at any scale on any point of the Brownian path, you will be able to follow the same "outline drawing" procedure. – Lee Mosher Jun 27 '22 at 15:49
  • I'm not sure that this question admits an objective and authoritative answer, but questions of scale fall under the general domain of geometry. If you are looking for a more specific area, maybe fractal geometry or dimension theory. – Xander Henderson Jun 27 '22 at 15:52
  • Your question should be what properties are independent of the scale. For example if it is just cardinality, just classical set theory would tackle some of these things. For example the cardinality of the interval $[0,1]$ is the same as that of the real numbers $\Bbb{R}$. Or even the natural numbers have the same cardinality as that of the rational numbers. In terms of topology we would have that an open disc of of small radius(any positive number) say of 0.00001 is homeomorphic to the entire 2d plane and so on. – Mr.Gandalf Sauron Jun 27 '22 at 15:55
  • In terms of "volumes"(measure) you can perhaps search that the Cantor set which has same cardinality as that of the entire real line, has $0$ volume. – Mr.Gandalf Sauron Jun 27 '22 at 15:56
  • @Mr.GandalfSauron My question is what different properties will emerge when on a different scale. That is, these properties are scale-dependent. – nevermind_15 Jun 27 '22 at 16:27
  • One way of interpreting your question is by analogy with the fact that sequences can have more than one cluster/limit point (e.g. 1, 2, 3). Roughly speaking, we can consider magnifications at a point as a sequence of compact sets in the Hausdorff metric (a way of defining distance between compact sets), and then consider issues (continued) – Dave L. Renfro Jun 27 '22 at 16:52
  • relating to the fact that sequences can have more than one limit point. Thus, a sequence of magnifications at a given point might have many different compact sets as subsequence limits. This notion appears in Buczolich's papers on micro tangents (e.g. 1, 2, 3) and the Gruber paper I mention in a comment here. – Dave L. Renfro Jun 27 '22 at 17:02
  • thanks, everyone I think I found it: https://royalsocietypublishing.org/doi/epdf/10.1098/rsta.2021.0150 – nevermind_15 Jun 28 '22 at 03:24

0 Answers0