Equation for a distorted circle

Question

When you view a circle posted on a wall at a distance and at a glancing angle, the circle elongates. However, I don't think it is just an ellipse because it will also become asymmetric. It has more of an egg-shape. (Please correct me if this assumption is wrong)

Is there a name for this kind of shape? What is it's equation?

(This is for a computer vision project in which I am thinking of detecting circular fiducials)

I looked at How to define a perspective circle in xy?, but the equation in the answer still seems symmetric about the y-axis.

... as it should be, because it's an ellipse. Google Image Search. — 40 votes, Jul 19 '13 at 00:48
Only if you assume that light enter parallel into your eyes. — user86828, Jul 19 '13 at 01:48
The diagrams in the Google image search are pretty convincing. But, it still confuses me why a square deforms into an asymmetric quadrilateral, whereas the circle deforms into a symmetric ellipse (just tilted). I think I need to study the properties of a perspective distortion more. — kdaquila, Jul 19 '13 at 05:19
The cone formed from the circle with the eye as vertex is still a quadric cone, even when the vertex is not on the axis of symmetry of the circle (as figure in space). The intersection of this cone with any plane is still a conic (quadric curve), so an ellipse if it’s compact. — Lubin, Jul 19 '13 at 20:30

40 votes · Accepted Answer · 2013-07-19T20:14:52.587

why a square deforms into an asymmetric quadrilateral, whereas the circle deforms into a symmetric ellipse

But the center of circle does not project to center of ellipse. If you color one half of circle (nearest to you) in red, you will see in perspective that more than half of the ellipse is in red. This agrees with the behavior of the square: the side near us appears larger.

Here is a picture which, according to Andrejs Treibergs, comes from Della pittura (1435) by Alberti. (It does not look that old to me, I guess it was re-drawn).

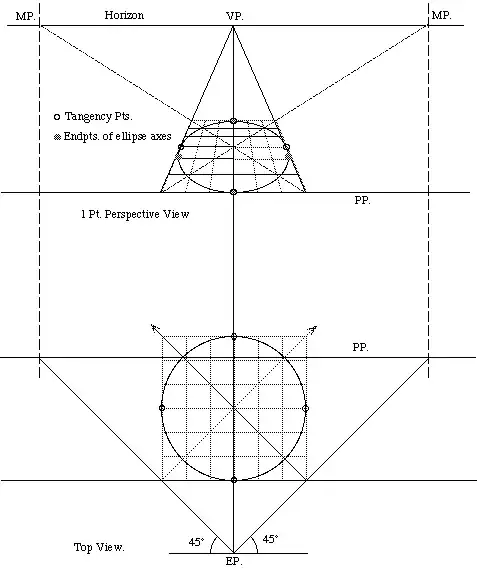
Circle in perspective

The center of the circle (below) is on the intersection of the diagonals of the square. Since collinearity is preserved in perspective, the center of the circle in perspective is on the intersection of the diagonals of the trapezoid above. When sketching this by hand, you would draw a horizontal line through this point to find where the ellipse is tangent to the sides of the trapezoid.

But this horizontal line is not the major axis of the ellipse (it's a typical novice mistake to think that it is). The major axis is below the line of tangency points; that is, the ellipse still gets wider after touching the trapezoid. On the diagram above, this effect is slightly exaggerated: the endpoints of the major axes should be marked a bit higher. But they definitely are below the tangency points.

I recommend this page (Mathematics of Perspective by Andrejs Treibergs) as a gentle introduction to the subject.

Wow! Thank you so much for this very clear explanation :-) – kdaquila Jul 20 '13 at 21:22 — kdaquila, Jul 20 '13 at 21:22

Equation for a distorted circle

1 Answers1