You can see a perspective view of a square(FCED) and a circle in 2D screen. O is center of the circle.
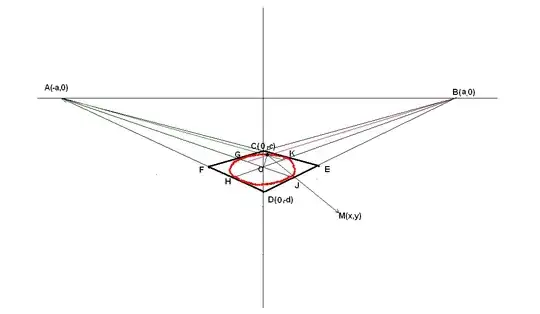
How can I define the perspective circle equation that shown as red in the picture?
Thanks a lot
You can see a perspective view of a square(FCED) and a circle in 2D screen. O is center of the circle.

How can I define the perspective circle equation that shown as red in the picture?
Thanks a lot
The red curve is an ellipse, but the point $O$ will not be the center of this ellipse!
The values $a$, $c$, $d$ seem to be given, and the figure is symmetric with respect to the $y$-axis. Intersecting $A\vee D$ with $B\vee C$ gives you the point $F=(-f,-g)$. It follows that $E=(f, -g)$ and $O=(0,-g)$. Intersecting $A\vee D$ with $B\vee O$ then furnishes $H$, and intersecting $B\vee C$ with $A\vee O$ furnishes $G$.
By symmetry the ellipse has an equation of the form $${x^2\over p^2} +{(y+m)^2\over q^2}=1$$ with unknown constants $p$, $q$, $m$. The coordinates of $G$ and $H$, through which the ellipse passes, provide more than enough information to determine these constants.
One possibility is to find out the projective transformation itself, then apply on the circle.
Were these objects originally really a square and a circle somewhere? I mean, can you use those data or only $a,c,d$?
Put the whole picture in 3d, on the $z=1$ plane (that is, $A=[-a,0,1]$, $B=[a,0,1]$, $C=[0,-c,1]$ and $D=[0,-d,1]$ will be). Then consider the matrix $$M:=[A|B|C]=\begin{bmatrix} -a & a & 0 \\ 0 & 0 & -c \\ 1 & 1 & 1 \end{bmatrix}$$ then $M\cdot\begin{bmatrix} 1\\0\\0 \end{bmatrix} = A$, $\ M\cdot\begin{bmatrix} 0\\1\\0 \end{bmatrix} = B$, $\ M\cdot\begin{bmatrix} 0\\0\\1 \end{bmatrix} = C$, so $M^{-1}$ takes $A$ and $B$ to the ideal points $i_x:=\begin{bmatrix} 1\\0\\0 \end{bmatrix}$ and $i_y:=\begin{bmatrix} 0\\1\\0 \end{bmatrix}$, and $C$ to the origo $\begin{bmatrix} 0\\0\\1 \end{bmatrix}$.
So, for this, you need to calculate $M^{-1}$, then $D':=M^{-1}D$ (divided by its 3rd coordinate) will give the opposite corner of the square, suppose $D'=\begin{bmatrix} u\\v\\w \end{bmatrix}$, then $u=v$ should hold (because it wants to be a square), and $F'=(u/w,0)$ and $E'=(0,v/w)$ will be [projected back to the $z=1$ plane].
Then form the circle (centered at $(u/2w,u/2w)$ with radius $u/2w$) in homogenious coordinates [-- so we could also call it a cone]: $$(\frac xz-\frac u{2w})^2 + (\frac yz-\frac u{2w})^2 = \left(\frac u{2w}\right)^2$$ and transform it back by $M$: $$(x,y)\ \text{ in the red ellipse} \iff M^{-1}\begin{bmatrix} x\\y\\1 \end{bmatrix}\ \text{in the circle} $$