Anti-dual numbers and what are their properties?

Question

In this post user William Ryman asked what would happen if we try to build "complex numbers" with shapes other than circle or hyperbola in the role of a "unit circle".

Here I proposed three shapes that could work. The common principle behind them being that if the unit curve is defined as $r=r(\phi)$, an arbitrary point, corresponding to a 2-dimensional number on the plane $z=(a,b)$ is characterized by angle $\alpha(z)=\arctan(b/a)$, magnitude $M(z)=\frac{\sqrt{a^2+b^2}}{r(\alpha(z))}$ and argument $\operatorname{arg}(z)=\int_0^{\alpha(z)} r(\phi)^2 d\phi$, twice the area of a sector between the radius-vector and $x$ axis.

The addition of numbers is defined element-wise as $(a_1,b_1)+(a_2,b_2)=(a_1+a_2,b_1+b_2)$.

The multiplication is defined in such a way that the arguments are added and magnitudes are multiplied: $\operatorname{arg}(uv)=\operatorname{arg}(u)+\operatorname{arg}(v)$ and $M(uv)=M(u)M(v)$.

These definitions make addition and multiplication commutative and associative.

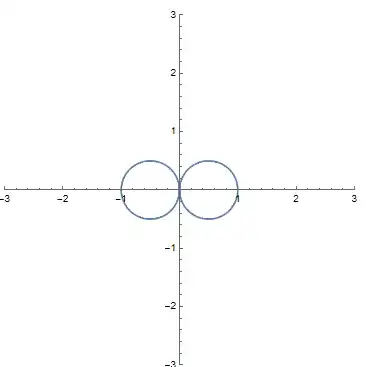
So, I decided to consider the number system based on the following equation for unit curve: $r=|\cos\phi|$ (which is two tangent circles). This function is reciprocal to the function defining dual numbers, so I called the system "anti-dual numbers".

The expressions for modulus and argument of a number $z=(a,b)$ thus would be:

$M(z)=\frac{a^2+b^2}{a}$

$\arg z=\frac{1}{2} \left(\frac{a b}{a^2+b^2}+\arctan \left(b/a\right)\right)$

These expressions are valid for the first quarter of the plane, in other quarters we should account that negative modulus corresponds to a shift of argument by $\pi/2$ (not by $\pi$ as in complex numbers!), that's why we have to add the functions arg and mod which are intended to represent the canonical form.

The expression for the angle of direction of radius-vector as a function of argument is from this post by Tyma Gaidash:

$\phi (z)=\arcsin\sqrt{I_{\frac{4 \arg z}{\pi }}^{-1}\left(\frac{1}{2},\frac{3}{2}\right)}$

This expression involves inverse beta regularized function.

The code below for Mathematica system provides functions for determining argument and modulus of a number $(a,b)$, determining Cartesian coordinates based on modulus and argument as well as a function that multiplies two numbers given in Cartesian coordinates.

arg[a_, b_] := 1/2 ((a b)/(a^2 + b^2) + ArcTan[b/a])
mod[a_, b_] := (a^2 + b^2)/a
argc[a_, b_] := arg[a, b] + Pi/2 HeavisideTheta[-mod[a, b]]
modc[a_, b_] := Abs[mod[a, b]] 
\[Phi][A_] := 
 ArcSin[Sqrt[InverseBetaRegularized[4 A/Pi, 1/2, 3/2]]] // FullSimplify
angle[A_] := 
 Piecewise[{{\[Phi][A], 0 <= A < Pi/4}, {\[Phi][A - Pi/4] + Pi/2, 
    Pi/4 < A <= Pi/2}, {-\[Phi][-A], -Pi/4 < A < 
     0}, {-\[Phi][-A + Pi/4] - Pi/2, -Pi/2 < A < -Pi/4}}]
X[m_, A_] := m Cos[angle[A]] Abs[Cos[angle[A]]]
Y[m_, A_] := m Sin[angle[A]] Abs[Cos[angle[A]]]
Multiply[{a1_, b1_}, {a2_, b2_}] := {X[mod[a1, b1] mod[a2, b2], 
   arg[a1, b1] + arg[a2, b2]], 
  Y[mod[a1, b1] mod[a2, b2], arg[a1, b1] + arg[a2, b2]]}

Example:

a := -1; b := -1
arg[a, b]
mod[a, b]

Output:

1/2 (1/2 + Pi/4) - Pi/2
2

Multiplication:

Multiply[{1, 1}, {1, 1}] // N

Output:

{-1.10363, 1.78788}

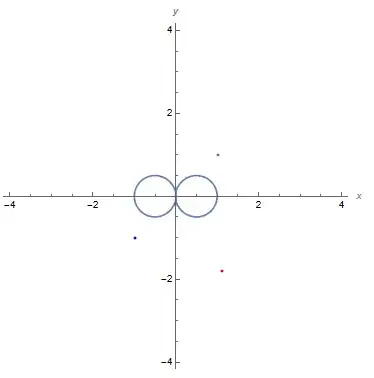
The following code makes plot of multiplication of two points:

p1 := {1, 1}
p2 := {-1, -1}
p := Multiply[p1, p2] // N
ContourPlot[(x^2 + y^2)^2 == x^2, {x, -4, 4}, {y, -4, 4}, 
 Axes -> True, AxesLabel -> Automatic, Frame -> None, 
 Epilog -> {Gray, Point[p1], Blue, Point[p2]}, Red, Point[p]]

---

That said, I wonder, what algebraic and analytic properties this system has? It seems to be a 2-dimensional hypercomplex commutative numbering system that is not isomorphic to complex, split-complex and dual numbers.

One interesting feature of this system is existence of divisors of infinity because $(0,1)(0,1)=\infty$ (multiplication by divisors of infinity cannot be handled by the provided code though). This makes the system not closed under multiplication unless an improper element $\infty$ is attached. On the other hand, the system has no zero divisors. The system is not distributive, though, despite being commutative and associative.

What else can be said about the system? Can analysis be built on these numbers?

Answer 1

Your unit-norm curve passes through zero. This means the norm is nor well-defined at zero, which then implies the norm is not well defined on some path through zero (which turns out to be the vertical axis). Lack of closure under multiplication arises from this condition.

Closure under multiplication required choosing a unit-norm curve that avoids zero.

Answer 2

$\DeclareMathOperator{arccsc}{arccsc}$ The power equation for $(a_1+b_1)^n=a_n+b_n\omega$ is $$a_n=\frac{\sqrt{(a_1^2+b_1^2)(a_{n-1}^2+b_{n-1}^2)}}{r(\alpha(\theta_1))\cdot r(\alpha(\theta_{n-1}))},\quad b_n=\sin(\alpha(z_{n-1}))+\sin(\alpha(z_{1})).$$ This is an idea of the equation, and I may have made some errors along the way. I used $z^n=M(a_1,b_1)M(b_{n-1},a_{n-1})+\arg(b_{1},a_{1})+\arg(b_{n-1},a_{n-1}).$ Expanding the general $M(a,b)$s gives you the formula for $a_n$, and using the general arg() instead of the specified equation, then using the FTC gives you $$\int_0^{\alpha(z_{n-1})}{|\cos(x_n)|dx_n}=\int_0^{\pi/2}{\cos(x_n)dx_n}+\int_{\pi/2}^{\alpha(z_{n-1})}{\cos(x_n)dx_n}\\ =\sin(\alpha(z_{n-1}))+\sin(\alpha(z_{1})).$$ The exponential and log can be found by using their taylor series', then use the exponential and logarithm definitions of other functions to define them. $$\frac{1}{z}=e^{-\ln(x)},\;\; \sinh(z)=\frac{e^z+e^{-z}}{2},\;\; \arcsin(z)=−i\ln{(iz+\sqrt{1−z^2})},\\ \arccsc(z)=\arcsin{\left(\frac{1}{z}\right)} \ldots$$ For arcsin() and other ln() based functions, use $\ln{\big((a+bi)(c+d\omega)\big)}=\ln(a+bi)+\ln(c+d\omega).$ I realized just now that $b_n\le2$ when $n\gt1,n\in\mathbb{N}$ For this specific pair, simplifying the original equation gives you $$\frac{a_{n-1}^2+b_{n-1}^2}{a_{n-1}}*\frac{a_{1}^2+b_{1}^2}{a_{1}}+\omega(\frac{b_{n-1}}{a_{n-1}^2+b_{n-1}^2}+\frac{b_{1}}{a_{1}^2+b_{1}^2})$$