In 1 dimensional space, to map an interval $[0,1]$ into another interval $[a,b]$ we use the function
$$T: [0,1] \to [a,b] :\quad x \mapsto (1-x)a+xb$$
What is the generalisation of this in 2D space (or higher), in other words, what is the function $T$ such that $T$ maps the square $\{(1,1);(-1,1);(-1,-1);(1,-1)\}$ into a quadrilateral $\{(x_1,y_1);(x_2,y_2);(x_3,y_3);(x_4,y_4)\}$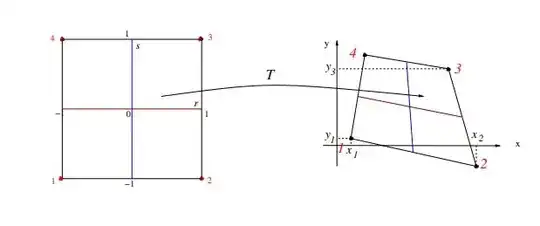
Asked
Active
Viewed 84 times
2
Hidda Walid
- 187
-
+1: Others may (deservedly) downvote your question, because of its defects, with respect to this MathSE article on protocol. I upvoted the question, despite the question's many defects because I find the posed question very intriguing. – user2661923 Apr 21 '22 at 21:41
-
Some answers and references at 1, 2. – dxiv Apr 22 '22 at 04:10